To view my slides click.  Slides

On page 262, Cleveland states that “Any data that can be encoded by one of these pop charts (such as a pie chart, divided bar chart or an area chart) can also be decoded by either a dot plot or multiway dot plot that typically provides far more pattern perception and table look-up than the pop-chart encoding.” Demonstrate that Cleveland is right by finding two pop charts in the media and redrawing each data by using a dot plot or multiway dot plot. In each case, show the original pop chart and the new plot and explain why the new plot is an improvement.

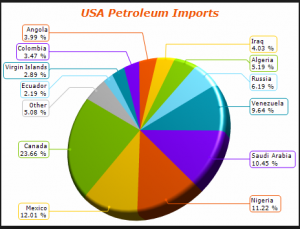
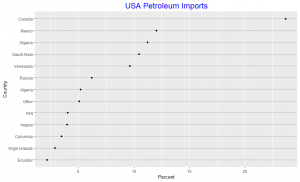
Since the slides in the pie chart are arranged in increasing order of percentages except the “other” category, we observe that the pattern perception for both the pie chart and the dot plot are very similar. We note the difficulty in visually obtaining the difference in percentages between the slides in the pie chart unlike in the dot plot. The dot plot gives an added information due to it’s position encoding as it detects that two different line segments could be used to represent percentages between 2.19 to 6.19 and 9.64 to 12.01 respectively, in this spirit we may consider the 23.66 percent import from Canada as an interesting outlier. Thus the dot plot is an improvement over the pie chart.

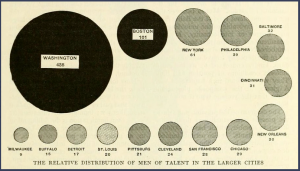
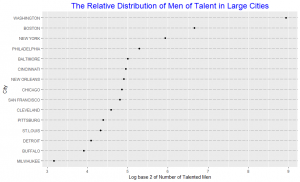
In the area chart, the area of each circle represents the number of talented people in that city. As we observe, it’s difficult to distinguish the difference in area for some of the cities without having to look at the numbers beneath them. One may argue that with the numbers beneath each circle the graph may as well be represented by just a frequency table. The area chart do not provide efficient detection of geometric objects that convey information about differences of values. The dot plot shows the number of talented people using a log scale. The data are graphed by position along a common scale and pattern perception is far more efficient than the area chart. For example, it is hard to detect a change in the circle areas for Philadelphia and New York just by looking at the area plot without looking at the number beneath the circle, but the dot plot shows that the numbers vary much. Table look-up is far more accurate and rapid from the dot plot than from the area chart. The matching operations necessary to decode values from the area chart are both slower and less accurate than the scanning and interpolation operations that provide table look-up from the dot plot. Hence the dot plot is an improvement over the area chart.

In this post we construct a scatterplot matrix, a coplot, and a spinning 3-dimensional scatterplot for Potassium, Fibre and Protein which are three variables in the dataset UScereal in the MASS package with eleven variables for a group of 65 breakfast cereals. Based on our graphs, we describe the general relationships between the three variables. In addition, we find two “special” cereals that seem to deviate from the general relationship patterns.

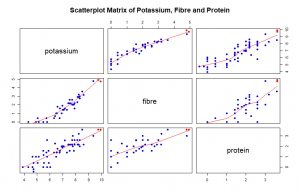
We plot log base 2 of the variables potassium, fibre and protein to improve the resolution of our plot, most data points were clustered at one side of the graph. From our scatterplot matrix we observe that the relationship between potassium and fibre, potassium and protein, fibre and protein is about a positive linear association. An increase in one variable saw an increase in the other.

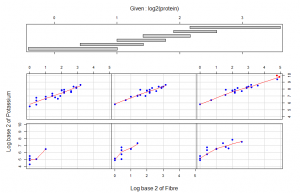
In the coplot also we plotted log base 2 of Potassium against log base 2 of Fibre while we condition on log base 2 of Protein. From the two panels at the lower left of the coplot we observe a nonlinear relation between the amounts of potassium and fibre in cereals when we condition on protein. From the lower left panel, below 1.414 of fibre in the cereals potassium is constant and above 1.414 of fibre there is a positive linear association. In the second panel from the lower left there is a positive linear association below 1.416 of fibre and a positive linear association above 1.416 of fibre as protein increased. The slopes are however different. We observe some interaction between protein, potassium and fibre. From panel (3,1), (1,1), (2,2) and (3,3) we observe a positive linear association between potassium and fibree. At this point no effect of protein is seen.

As fibre increases potassium increases. Protein increases and stops at around a height of 10. Two special cereals with Protein above the normal protein levels for all cereals and corresponding to the highest levels of fibre and potassium which deviate from the general relationship pattern are 100% Brand and All – Bran indicated with red in all the plots.

In the first part of this post I will construct four time series plots on the same graph and in the second part I will choose a nice palette for a bivariate normal density estimate. The data set for the time series plot is the Broadway show from https://think.cs.vt.edu/corgis/csv/broadway/broadway.html and the data for the bivariate normal denstiy estimate is simulated.

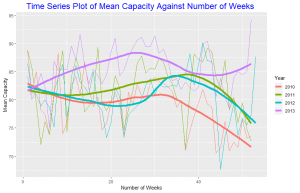
In the time series plot above we plot the mean Capacity as a function of week number, comparing years from 2010 to 2013. The choices help to distinctively distinguish the series for each year. A loess curve is overlayed on each year’s series. At the beginning of 2010 the mean capacity was 82.5, this decreased from the first week till the 13th week and then increases till the 30th week and also decreased from there till the 52nd week recording a mean capacity of about 71. In 2011 mean capacity decreased from the first week till the 9th week and increased till the 32nd week. 2012 shows a similar pattern as 2010. 2013 was interesting to look at, mean capacity increased from the first week till about the 25th week then decreased till about the 38th week and increased till the end of the year.

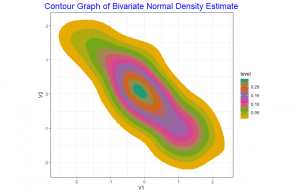
In the contour graph of the bivariate normal density estimate we use the palette “Dark2”. With this we are able to see clearly each of the contour curves well. The contour curves are ellipses. The negative slope of the major axis shows the negative correlation between the two variables and its eccentricity shows the correlation value is close to -1.

In this post I will be presenting scatter plots overlayed with Loess smoothing curves and their residual plots. Data generated from a simulation is used for the plots.

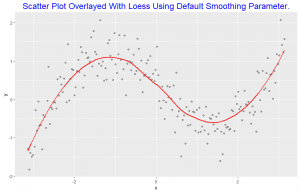
This scatter plot is overlayed with loess smoothing curve with the default smoothing parameter of 0.75.

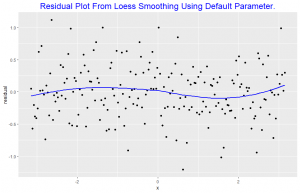
The residuals are graphed against x and a loess curve is superposed; for the curve on this display, alpha = 0.8. The loess curve suggests there is some dependence of the residuals on x, since the curve is not nearly horizontal. This means the default smoothness parameter is too large in the smoothing of the scatter plot above. This indicates that the loess curve has not effectively found the signal.

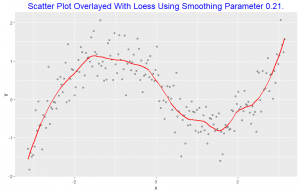
The scatter plot is overlayed with loess smoothing curve with smoothness parameter of 0.21

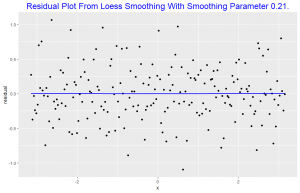
This plot shows no dependence of the residuals on x, since the loess curve is horizontal. This suggests the loess curve with smoothness parameter 0.21 overlayed on the scatter plot is not distorting the underlying pattern. This indicates that the lowess curve has effectively found the signal. For the loess curve in this plot alpha = 0.8.

In this post I will be constructing three dotplots. I will use data in a two-way table to construct these dotplots. The population of  8 Countries in West Africa namely Cote d’Ivoire, Ghana, Liberia, Mauritania, Mali, Niger, Senegal and Togo from 2008 through 2017 is cross classified in my two way table where response is the population, the row classification is Country and the column classification is Year.

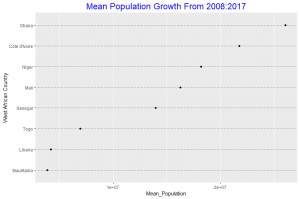
In this plot we observe that the mean population growth of Ghana over the 10 year period is the highest among the 8 countries considered. Mauritania has the least mean population growth which is not too different from the mean population growth of Liberia.

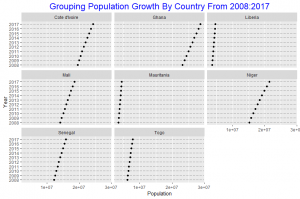
Grouping by country Ghana is seen to have experienced the highest population growth over the 10 year period. The population growth of Mauritania and Liberia are about same, these two Countries experienced the least growth over the 10 year period. The other countries also experience increase in population growth over the 10 year period.

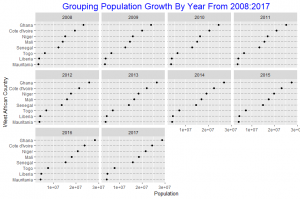
Grouping by Year, much more insight is gain on how each Country’s population grew compared to the others from year to year. From 2008 to 2017 Ghana is seen to maintain its lead in population growth at higher rates compared to the other countries. Liberia and Mauritania did not experience much increase in population growth from each year to the other. The other countries did increase.

When we grouped by year ( column variable) we are able to compare the population growth of all countries for each time period, but when we group by country ( row variable )  comparison is quite challenging, we see mainly how each country’s population grew over the 10 year period. Grouping by year seems to give us more insight into comparison and thus I will consider grouping by Year ( the column variable ) as better.

In this post I will be comparing distributions of data using a one-dimensional scatterplot, a Quantile plot, Quantile – Quantile plot and Tukey mean difference plot. The dataset used for this is studentdata from the LearnBayes package which contains results from a survey given to a large group of students from an introductory statistics class. A random sample of size 100 is taken from the data with variables Haircut and Gender.

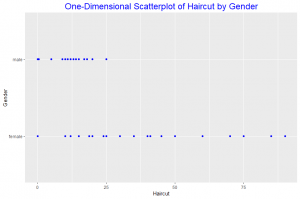
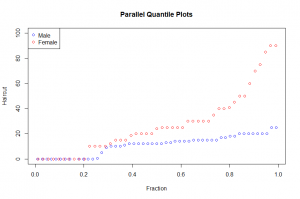
The one-dimensional scatterplot shows the distribuition of the male and female haircut. Female haircut was more than male haircut. From the quantile plot we observe that in the 0.2 quantile both male and female haircut was zero. The median of the Haircut for females is about 25 and that of males is 10. Comparing haircut for the 0.95 quantile we observe that male haircut is slightly less than 20 whiles that of females is about 70. Thus comparing the two distributions of the data we see that female haircut was more than males.

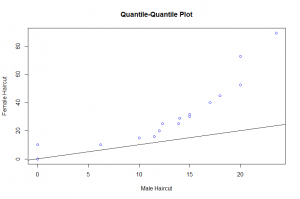
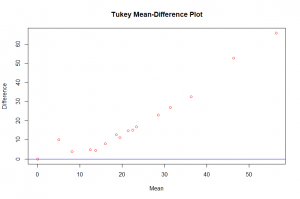
Throughout the entire range of the distribution, the female haircuts are greater than the male haircut as seen in the quantile – quantile plot. The relation between the two distributions can best be discribed by an exponential function. From the Tukey Mean-Difference plot we observe that the difference of the haircuts across all quantiles was positive and increased as the mean haircut increased. Also indicating that female haircut was more in all the quantiles.

The quantile-quantile plot of the measurements is the best display to compare the distribution of the haircut for males and females. Not only are we able to compare each quantile of male haircut and female haircut but we are also able to state a relationship by use of a function between the two measurements by looking at this graph which the other displays can not readily give.

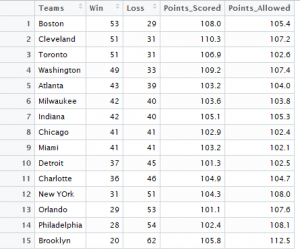
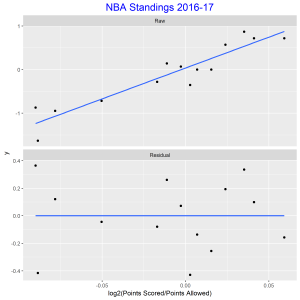
The data used for the graph is NBA standings for 2016-17 for the Eastern Conference. The first panel is a scatter plot of log2(win/loss) against log2(points scored/ points allowed) overlayed with a line of best fit. There is a positive association. The best fitting choice for k is 14.148. We did not observe any unusual teams from the residual plot. A standardized residual plot was also constructed which showed that all points were within two standard deviations of the mean indicating that there were no unusual points.

• Visualizing Amounts

In this post I will be comparing the best Broadway shows for two time intervals: 2000-2008, and 2009 – 2016. I will be using total attendance for Broadway shows over the two time intervals as my measure of best. I will present four grouped and stacked bar graphs, the first two needs some improvements and the final two are the improved versions of the former. The data for the plot can be access at  https://think.cs.vt.edu/corgis/csv/broadway/broadway.html

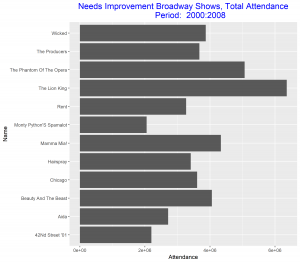
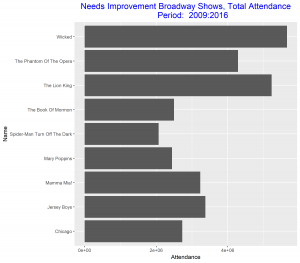
Since our aim is to compare the best Broadway shows over the two time intervals, we can improve these two graphs above be arranging the bars in each in a decreasing order. We also relabel the vertical axis to make it more descriptive of our data. These improvements will make the graphs stand out and good to be used for our comparison.

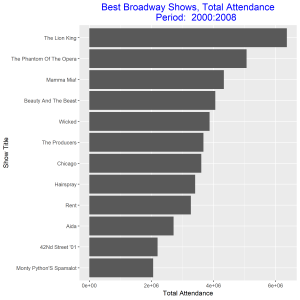
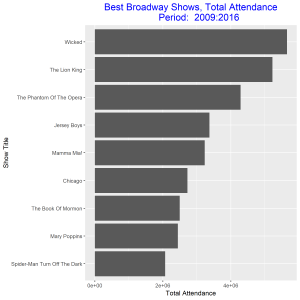
From the improved graphs we observe that the best Broadway show from 2000 – 2008 was the show with title “The Lion King” and the best in 2009 – 2016 was the show with title “Wicked”. The total attendance for the best show in 2000 – 2008 was greater than the total attendance for the best show in 2009 – 2016. The show title “The Lion King” came out as the best out of eleven other competitors as against the show title “Wicked” which came out as the best out of only eight competitors. The least best Broadway shows were “Monty Python’s Spamalot” and “Spider-Man Turn off the Dark” respectively for the two time intervals. Both gained this position with about the same total attendance.

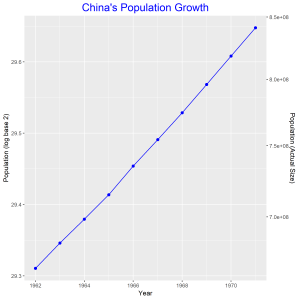
The graph above is a plot of China’s population growth from 1962 to 1971. The log base 2 of the population is on the left vertical axis and the actual population size is on the right vertical axis. The plot of the actual population against year shows and exponential growth in population. Taking log base 2 of the population and plotting it against year gives a linear graph. From the graph we observe that China’s population increased by 26.6% over this 10 year period.

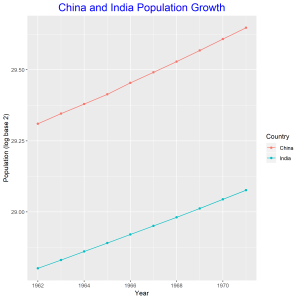
In this graph we compare the population growth of China and India. The log base 2 of the population is plotted against year, hence the linear graphs. China’s population is increasing at slightly higher rate than that of China. The intercepts of the two graphs shows that China’s population is higher than that of India.

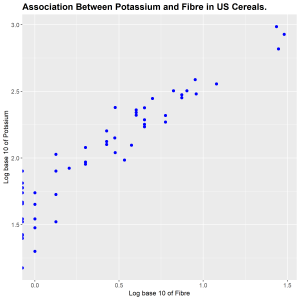
A correlation matrix of the numeric variables in the dataset, UScereal in the MASS library, is formed together with a scatterplot matrix using all the variables.  The highest correlation is between potassium and fibre.  On the horizontal scale log base 10 of fibre is plotted and on the vertical scale log base 10 of potassium is plotted. The log base 10 of each variable is plotted to stabilize the variability in the data. Plotting the log of the data also helped to make use of more of the data rectangle making the data standout. We observe a positive association between the two variables. As the fibre in the cereal increases the potassium in the cereal is also increased. We encountered a challenge with taking log since there were some observations which were 0, resulting in some points on the vertical scale.

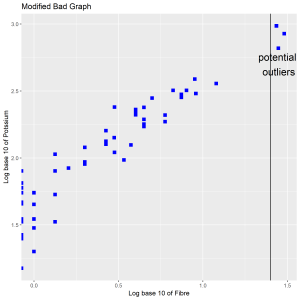
We violated visual prominence by using squares to show the data. The overlap between the squares makes it difficult for the data to standout. Including a text and a reference line are needless in this plot (superfluity).

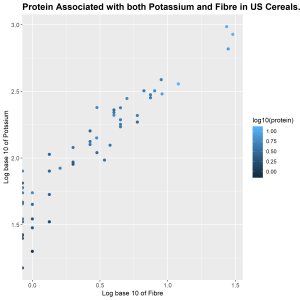
Protein is seen to be the most correlated variable to both potassium and fibre from the correlation matrix. From the plot we observe that there is a positive correlation between these  three variables. As fibre increases and potassium increases, protein also increases. The lower left corner of the plot has more dark blue points but moving further to the right more light blue colors are seen which represents increase in protein.

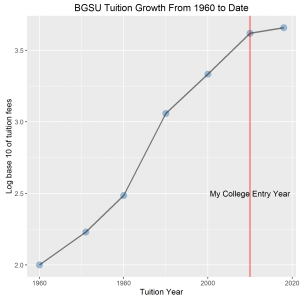
BGSU Tuition years from 1960 to date are plotted against tuition fees over the same period.  The graph shows a positive correlation between tuition year and tuition fees. The steepest slope is observed between 1980 and 1990 representing the greatest increase in tuition fees. The least increase in fees is seen from 2010 to 2018.

Welcome to blogs.bgsu.edu This is your first post. Edit or delete it, then start blogging!

Motor Trend magazine collected the horsepower and mileage for 32 cars in the 1973-74 model year. To see if there is any relationship between horsepower and mileage, I construct a scatterplot of the two variables.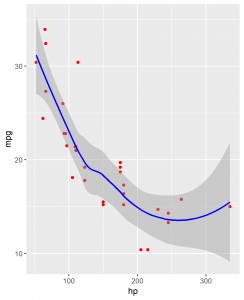

The graph shows a negative association between horsepower and mileage. As horsepower increases mileage decrease.