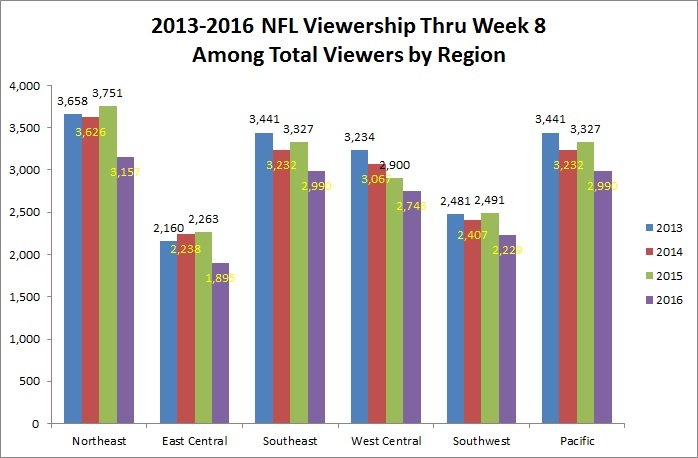
This week we are examining how to effectively use color to enhance the communication of the data. First, we will examine some time series data from the Broadway attendance data set. I chose four of the most popular shows, “Wicked”, “Lion King”, “Mamma Mia!”, and “The Phantom Of The Opera”, and plotted their weekly attendance as a percentage of the total capacity for the years 2012-2015.

We can see that in each of the years “Wicked” had busier periods in the summer and over the Christmas holidays. The color palette used is the default one in ggplot2.

For “Phantom of the Opera” we see a similar trend, with the summer drawing the most consistent crowds, and an even more precipitous spike in attendance over the Christmas holidays. The color palette used is “YlOrRd”. It is somewhat more difficult to differentiate between years, so I would not recommend using this one.

“Mamma Mia!” shows the same Christmas attendance jump, but less of the summer rise, with the exception of the last year it ran, 2015. The color pallet used is “RdYlBl”, which does a pretty good job of setting the years apart.

Finally, “The Lion King” uses the “Dark2” color palette, which is not as effective as the default palette and the “RdYlBl” palette, as it is difficult to tell the colors representing 2013 and 2015 apart. In addition, I realized when making this graph that it appears the attendance in the spring and fall have very dramatic drop-offs, but in reality the graph uses a different y-axis scale.
When a similar scale is used, we can see that the “Lion King” actually had by far the highest average capacity throughout the year, with the majority of shows sold out or very close to selling out.
Overall, I appreciate the default color palette in ggplot due to the ease of telling apart different categories by their color. In general, it seems choosing color spectrums such as the “YlOrRd” isn’t as effective in allowing the reader to differentiate categories.
Now we are going to examine color in the use of a contour plot.
Below is similar data in a contour plot, graphed with different color palettes.
The palettes I tried that did not have a gradient to them I found to be ineffective. In this data the color is representing the density of the distribution, so it should enhance the reader’s ability to interpret the graph. Trying palettes such as “Dark2” or “Spectral” did not yield effective graphs, as the different colors were not assigned to densities in any logical manner.

I found the “Grey” option to do a good job representing the levels of density. I tried inverting the gradient, but found the edges to be hard to distinguish from the grid. The benefit of this palette is that it is easy to reproduce on black and white printing.

My favorite palette I found was the “RdBu” palette. There is something natural about having red represent the “hottest”, or in this case, densest, areas of the distribution. In some ways, this choice of color functions like a heat map. The colors help communicate the rising levels of density to the reader of the graph.

Finally, I tried the “RdYlGn” palette. I visually find this choice effective in highlighting the different and rising levels of density as we approach the center of the graph, but aesthetically I don’t appreciate this palette as much.
If I were using a palette in a paper or assignment where I was graphing similar contour plots I would choose either the “Grey” palette or the “RdBu” palette, as these have both aesthetically pleasing qualities and helpful visual logic.