I was assigned to read the following three articles by Howard Wainer:
Graphical Birth Announcements—VOL.10, NO.2, 1997
Reporting Test Results to Institutions and Nations–VOL.15, NO.2, 2002
Finding What Is Not There through the Unfortunate Binning of Results: The Mendel Effect—VOL.19, NO 1,2006
As required, I summarize the first two articles and make a presentation. The link is below:
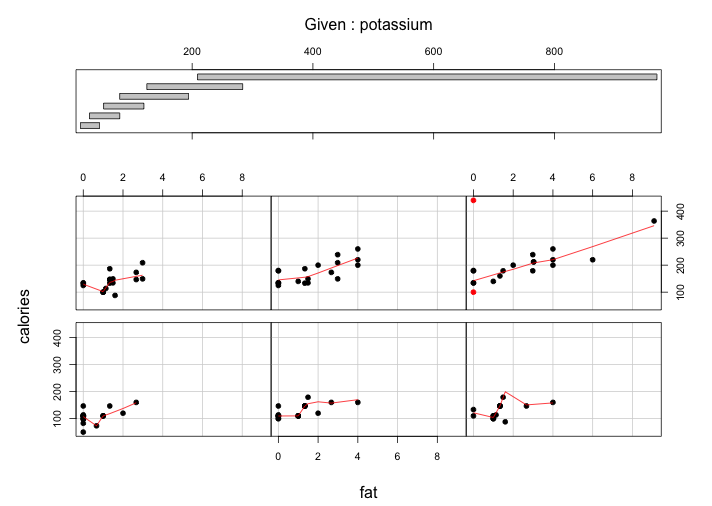
According to the requirement, I choose two graphs from my previous blogs and reconstruct them by ggplot2. The first one, a coplot of variables “reputation” and “a.grad.rate” in conditioning on Tiers, comes from the week13 color. The original graph is below: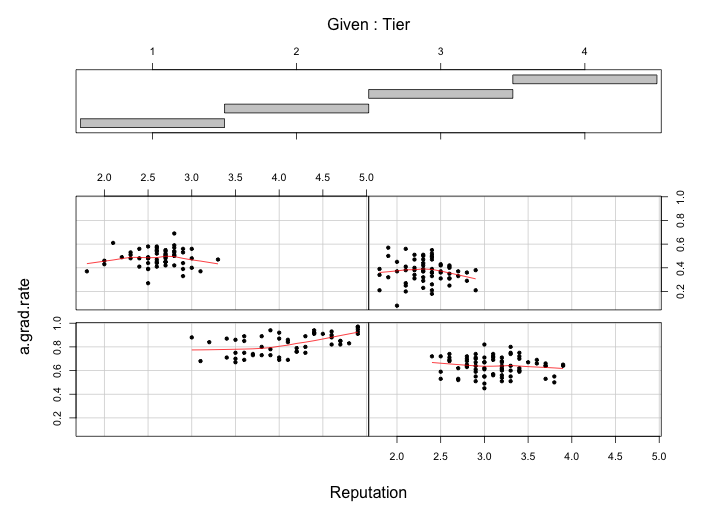
The panel at the top is the given panel, which is tier; the panels below are the dependence panels, which are Reputation (horizontal) against a.grad.rate (vertical). Each rectangle on the given panel specifies an interval of tiers. On a corresponding dependence panel, a.grad.rate is graphed against Reputation for those observations whose values of tier lie in the interval; a loess curve has been added to the panel, which produces smoothed values at any desired collection of values along the x scale and summarizes how y depends on x. If we start at the (1,1) dependence panel, the leftmost panel in the bottom row, and move form left to right in the row, then from left to right in the next row, and so forth, the corresponding intervals of the given panel proceed from left to right and from bottom to top in the same fashion.
For the four tier intervals, the patterns on the corresponding dependence panel are somehow different. The conditioning on tier has a linear pattern(if not too picky). For the (1,1) panel on the corresponding dependence, reputation ranges from 3.0 to 5.0 and a.grad.rate ranges from 0.7 to 1.0, although from reputation 3.0 to reputation 3.5, it seems a close to flat slope, we can still treat the whole interval as a positive linear relationship. For the (1,2) panel, the reputation ranges from 2.5 to 4.0 and the a.grad.rate ranges from 0.4 to 0.8, the overall trend is an almost flat. For the (2,1) panel, the reputation ranges from 1.8 to 3.3 and the a.grad.rate ranges from 0.3 to 0.7, the overall trend is almost flat line. For the (2,2) panel, the reputation ranges from 1.8 to 2.9 and the a.grad.rate ranges from 0.15 to 0.6, the overall trend is still almost an flat line.
However, I redraw the graph with package ggplot2 and get even better graph: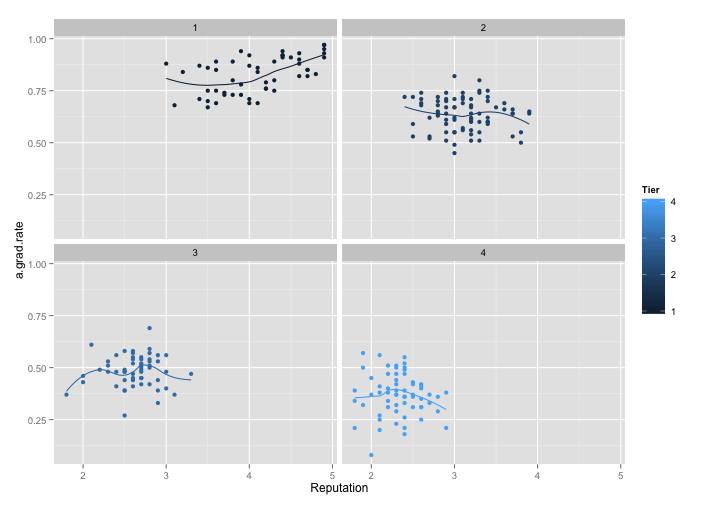
From the above graph, we can see that without a top given panel, the four panels give us a clear vision of Reputation versus a.grad.rate under each Tier label, which are divided 4 levels blue hue. In this way, not only the points can be easy recognized, but also the loess smooth lines. For visualization stand point, color is a powerful tool for encoding data, and it genuinely enhances the visual decoding of information from data displays and makes the visual operation of assembly as efficient as possible. In addition, without the top panel, we can treat the 4 panels as a whole and do not need to look back and fourth for the Tier information. Moreover, from this new graph, we can see more detail of the trend change for each Tier. Especially for the Tier3, which is fluctuated in the (1,2) panel in the new graph. Also, for Tier 2 and 4, there are somehow decreasing instead of a flat line. Overall, I prefer the ggplot2 display, based on graph efficiency, visual decoding and detail information.
From the same blog week 12 color, the first one is a scatterplot with 4 color: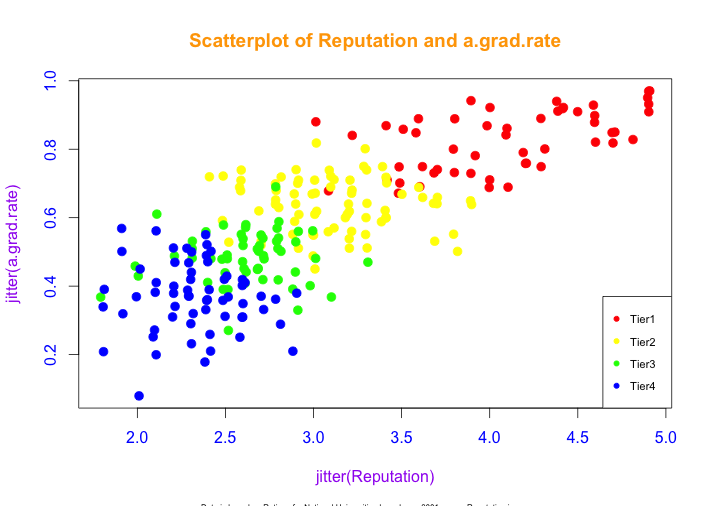 
From above graph, we can see that as reputation score increases, the a.grad.rate increases as well, corresponding from Tier 4 to Tier 1. The result means the better reputation, the higher a.grad.rate. Also, I use four different colors, red, yellow, green and blue to represent Tier1, Tier2, Tier3 and Tier4, respectively.
Then I use ggplot2 reconstruct the same graph: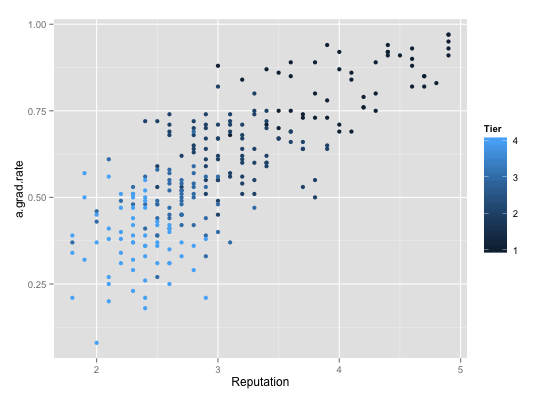
This graph use four level of cyan hue to Tiers: from dark(Tier1) to light(Tier4). However, if only based on color choosing, I prefer the original one. According ot HSL and HSV model, choose three primary colors-red, green and blue at first. If additional color needed, I will pick one of these secondary colors, such as yellow, orange, and purple and so on. For the new graph, it seems hard to identify the four levels of cyan hues, especially for non visual training people. However, if we change the default color setting, I think the new ggplot2 will be better, due to its additional grid line and legend outside, which will improve the visual decoding of the data information.
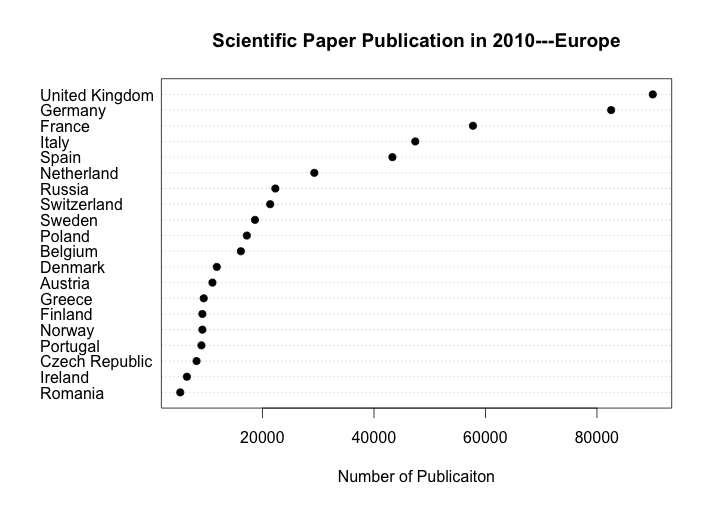
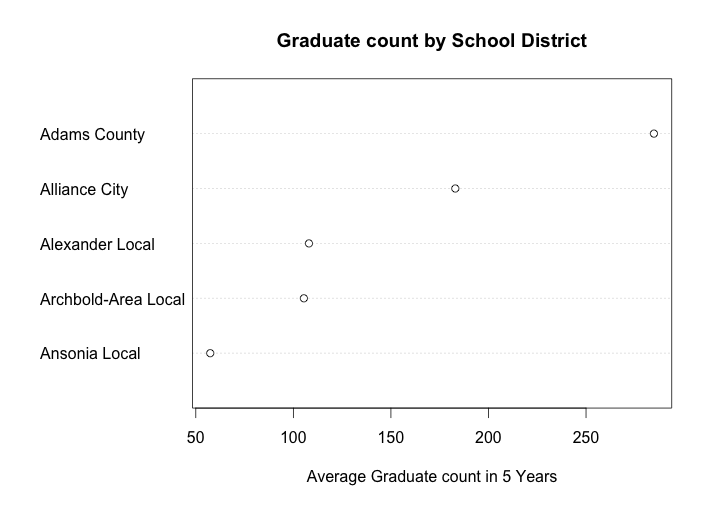
For more cases, the Second one, a dotplot of the average high school graduate count (# of people) in 5 years (from 2006 to 2010) for 5 Ohio school districts, comes from the week 8 dot plots. The original graph is below: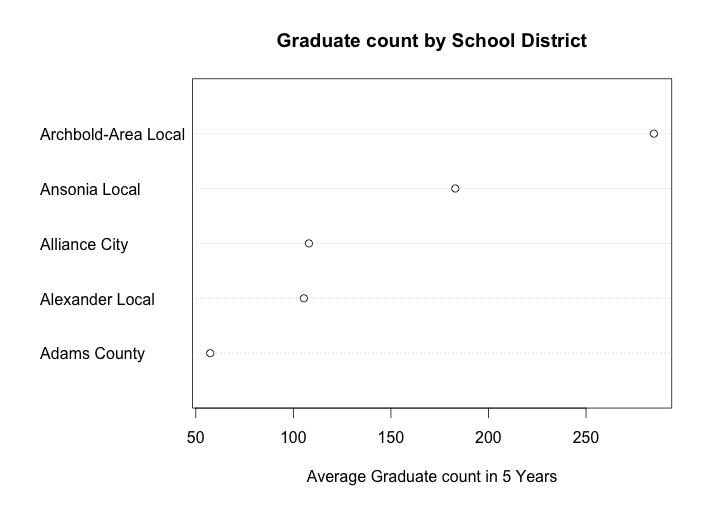
this graph is the average high school graduate count (# of people) in 5 years (from 2006 to 2010) for 5 Ohio school districts, which are Archbold-Area Local, Ansonia Local, Alliance City, Alexander Local, and Adams County. Since my data is ordered from high to low by row (School District), the distribution of the average high school graduate count of 5 school districts is showed in above graph. We can see that the school district “Adams County” has the highest 5-year average high school graduate number, which is close to 300. We can interpret that this school area either has a large population, or the reputation in this school area is very good, which attract many students to enroll in. Also, the school district “Ansonia Local” has the smallest 5-year average high school graduate number, which is barely above 50. We may interpret that this area has less population than other school districts.
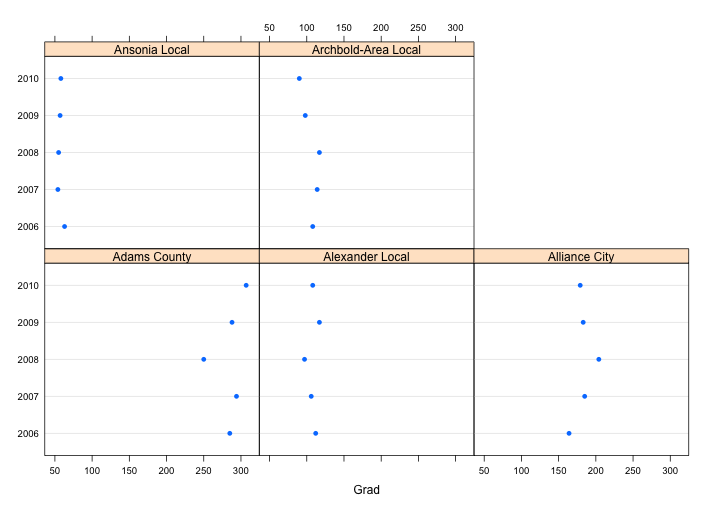
Same as the last example, I redraw the graph with package ggplot2 and get a better graph: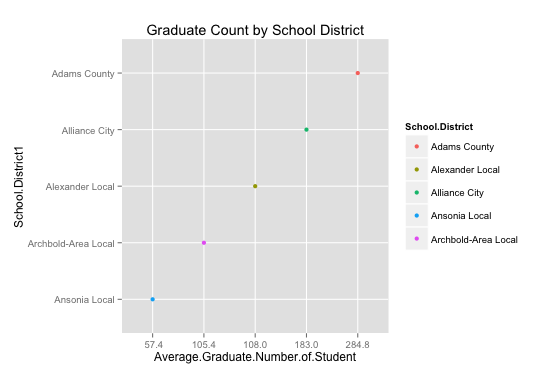
With the same data, we can see that by adding both horizontal and vertical grid line, we can see exactly the average it is. For example, the 5-year average graduate for Ansonia Local School District is 57.4, which is the lowest one, and the 5-year average graduate for Adams County School District is 284.8. Comparing to the first dot plot, the new one by ggplot2 has exact tick mark label, colorful points represent different school district, and improved grid lines, which are genuinely enhances the visual decoding of information from data displays and makes the visual operation of assembly as efficient as possible. (one problem is the distance between each tick mark label is equally divided, but the actual numbers are not. However, it does not affect our interpretation of the graph.) In this case, I prefer the ggplot2 graph, which gives us a better visual display and make the data stand out.
As semester approaches to the end, for dear readers who continue support my blog, I make an additional one for you to compare and thank you for your kind word and appreciation. This is one is stripchart(distribution) plot from week 7, distribution. The original graph are: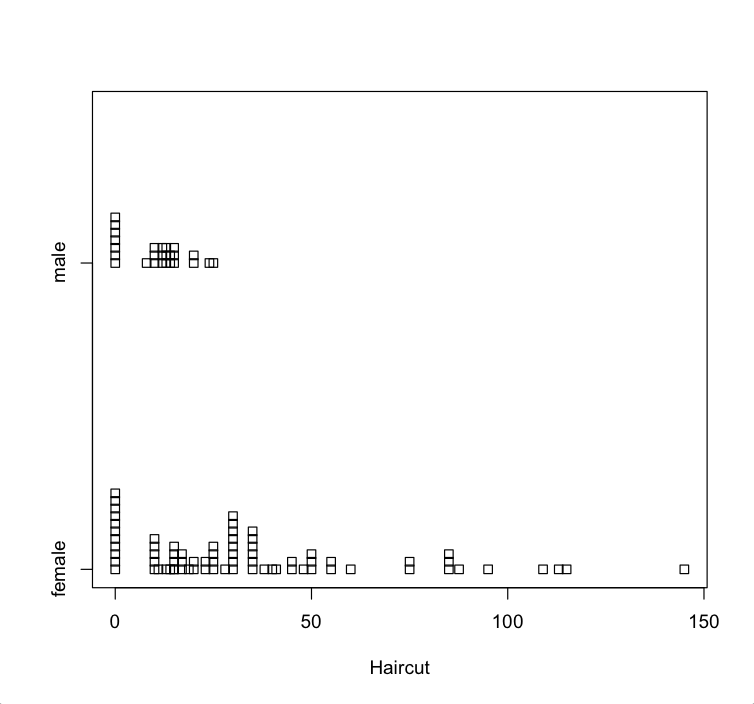
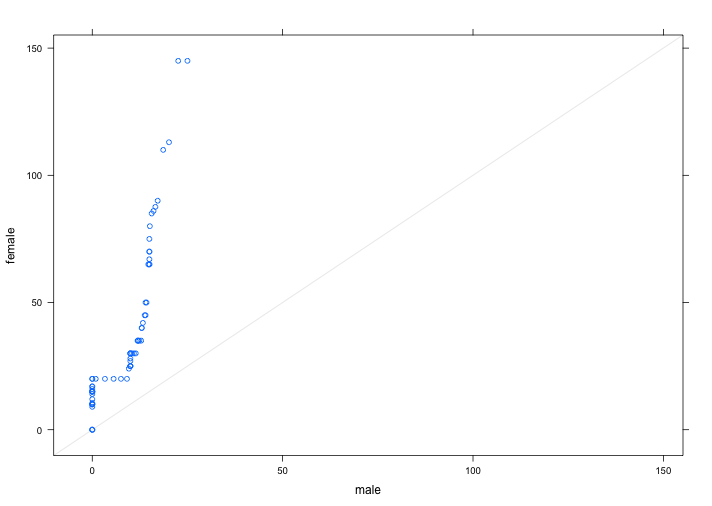
From the parallel stripchart we can compare the distribution of two groups of students and see that male students’haircut prices have narrow range, which is from 0 to 25 dollars. However, female students’ haircut prices have very wide range, which is from 0 to 145.On one hand, there are one third of male students(11) do not spend any money on haircut and almost half of male students(16) spend from $10 to $15, and only two male students spend more than $20 on haircut. The maximum money spend spends on haircut for male student is $25. On the other hand, over two third (47) of female students spend from $10 to $50 on haircut. Three females do not spend any money on haircut and only 4 female students spend more than $100. The maximum money spends on haircut for female student is $146. The distributions of these two groups are quite different.
However, I use ggplot2 package redraw another distribution plot, which can be see below: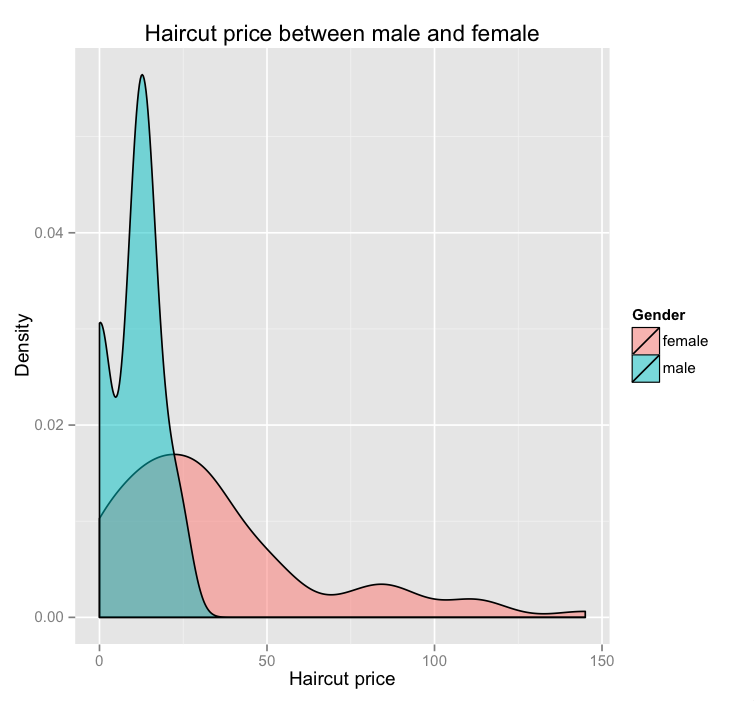
With the same data, we can see that there are two distributions cover different areas. As the data label showed, the pink represents female students and cyan represents male students. Based on this graph, the male student distribution is more concentrated compared to the female student distribution, which is more spread out and right skewed. On one hand, since this is a density graph, we can see that majority of male students spend between 10-15 dollars and majority of female student spend between 10 to 50 dollars. The extreme expense of female student is close to 150 dollars, while the maximum of male expenses is only close to 30 dollars. On the other hand, from the original graph, we can see exactly how many people spend how much money on haircut by counting the cube. The new ggplot2 graph, we can only see the density and overall distribution trend. Also for visualization standpoint, color is a powerful tool for encoding data, and it genuinely enhances the visual decoding of information from data displays and makes the visual operation of assembly as efficient as possible. Since I would like to know the overall trend and enjoy color visual display, I prefer the new ggplot2 graph, how about you?
In sum, ggplot2 is a plotting system for R, based on the grammar of graphics, which tries to take the good parts of base and lattice graphics and none of the bad parts. It takes care of many of the fiddly details that make plotting a hassle (like drawing legends) as well as providing a powerful model of graphics that makes it easy to produce complex multi-layered graphics. In most cases, ggplot2 will give us better visual decoding graphs.
R-code:
Rep.matrix=as.matrix(college.ratings[, c(2,4,6)]) Rep.matrix mine =data.frame(Rep.matrix) color library(ggplot2) m = ggplot(mine, aes(Reputation, a.grad.rate, color=Tier))
# panels. We do this by means of the facet_wrap() function. m + stat_smooth(se=FALSE, method=loess) + geom_point() + facet_wrap(~Tier)
# Distribution
qplot(Haircut,data=d.sample,geom="density",fill=Gender,alpha=I(.5),
main="Haircut price between male and female",
xlab="Haircut price",ylab="Density")
# dotplot
# default plot# the variables are alphabetically reordered.
m1.matrix=as.matrix(Book1)
mine1 =data.frame(m1.matrix)
m2 = ggplot(mine1, aes(Average.Graduate.Number.of.Student, School.District, color=School.District))
m2 + geom_point()
#reorder by average graduate number
mine1$School.District1 <- factor(mine1$School.District, levels=c("Ansonia Local", "Archbold-Area Local", "Alexander Local", "Alliance City", "Adams County"))
ggplot(data=mine1, aes(y=School.District1, x=Average.Graduate.Number.of.Student, color=School.District))
+geom_point()+labs(title = "Graduate Count by School District")
On April 4, 1964, the top five songs on the Billboard Hot 100 were all Beatles songs. The title of these songs are :
No. 1, “Can’t Buy Me Love”
No. 2, “Twist and Shout”
No. 3, “She Loves You”
No. 4, “I Want to Hold Your Hand”
No. 5, “Please Please Me”
As you see, the first part is only the fun fact to remark the 50 years anniversary of the big success of Beatles. The following part are more related to today’s topic: Pop charts.
“Any data that can be encoded by one of these pop charts (such as a pie chart, divided bar chart or an area chart) can also be decoded by either a dot plot or multiway dot plot that typically provides far more pattern perception and table look-up than the pop-chart encoding.” Now I will use two cases to demonstrate his word.
The first case of pop chart is a pie chart of Brower usage on Wikimedia, the graph is collected from Wikimedia.org
Browser usage on Wikimedia, March 2012
The pie chart that graphs 7 different Browsers that used on Wikimedia. The labels, 7 Browsers’ name, are categorical variable. We can see that Android Browser seems the least use, however, it is hard to say which one is the most use, IE or Chrome, whose area of segments are similar. Also, we are hard to identify the specific use of each Browser.
The following graph (the first one) is a dot plot of the Brower usage on Wikimedia. On one hand, the pattern perception is far more efficient for this display than for the pie chart. We can effortlessly see a number of properties of the data, for example, we can easy detect and cluster the line segments between the three dominant Browsers— IE, Chrome and Firefox and the three least use Browsers—Opera, Android and other. Also, it is easy for us to get an approximate difference (about 25%) between two clusters of Browsers. There is no corresponding detection operation for the pie chart that allows effortless decoding of differences. This result is degraded pattern perception of Pie chart. In addition, the line segment estimation was found to be more accurate than the sector size estimation, and this was assumed to be the fundamental issue for the poorer pattern perception from Pie chart encoding. But the fundamental issue is the efficient detection of differences of values for position along a common scale, which cause of the better estimation.
The following graph, I draw another dot plot with ordering the percentage from largest to smallest, which gives us a better visual decoding for the graph, while keep other good properties as the non-ordered one. The order of the categories for each categorical variable is an important aspect of the dot plot display method that substantially affects our visual decoding. Moreover, ordered data graph is more informative than non-ordered one. On one hand, when we study a distribution of values such as the enrollment of different universities, we want to know what is large, what is medium, and what is small. The organization in ordered data graph allows us to easily assemble and estimate the large values, or the medium values, or the small values. On the other hand, we cannot do this nearly as effectively in non-ordered data graph, because each of these sets of vales is scattered throughout the graph. It is easier to assemble the large values because they are spatially grouped by the ordering, and estimation is more accurate because the symbols encoding the values are closer to one another.
The second case is an area chart of scientific paper publication in 2010. The graph is collect from the following website.
The area chart of scientific paper publication in 2010 http://phytophactor.fieldofscience.com/2011/12/were-number-one-were-number-five.html
The area chart includes the top 40 countries by number of research papers published in 2010. For simplicity, we only focus on the Europe part. For that part, the area chart encodes the number of research paper publication of 20 Europe countries by the areas of circles. From the graph, we can easily identify that UK, Germany and France the largest three circles. However, the area charts do not provide efficient detection of geometric objects that convey information about the differences of values.
The above graph is a dot plot of scientific paper publication in 2010 with ordered number of publication. The data are graphed by position along a common scale and pattern perception is far more efficient than the original area chart. For example, since all the circles are placed by geographical location on map, it is hard to detect the difference in the circle area from Greece, Finland, Norway, to Ireland and Romania, but the ordered dot plot shows that the number of publication vary by a comparable large factor. Moreover, table look-up is far more accurate and rapid form the ordered dot plot than the area chart. Although every circle has the number of publication on it, the geographical location limited the space of data label display and plotting symbols are not sufficiently visually distinguishable form the label. In this case, the matching operations necessary to decode values from the area chart are both slower and less accurate than the scanning and interpolation operations that provide table look-up form the ordered dot plot. Also, the reason that I use order on dot plot is listed above.
In sum, the dot plot provides far more efficient pattern perception and table look-up than the pop-chart encoding. These two cases well demonstrate Mr. Cleveland’s word.
Part A:
The data frame college.ratings in the LearnEDA package provides ratings of a group of national universities based on 2001 survey data.
Based on the original data, I choose the variable “Reputation” and variable “a.grad.rate”, which represent “measure of academic reputation” and “percentage of freshmen who graduated within a six-year period”, respectively. The reason I think they are highly associated is because I believe the people who attain better universities not only have high talent, high self motivation and better study method, but also have stable financial support. These factors will help them graduate within 4 or 5 years regular time ranges successfully. In this case, the better university (high reputation), the higher a.grad.rate, vice versa.
After I construct the scatterplot with different colors for the different 4 Tier groups, I find that the graph confirms my believe, that reputation and a.grad.rate have positive relationship, nearly positive linear relationship if not too picky.
From above graph, we can see that as reputation score increases, the a.grad.rate increases as well, corresponding from Tier 4 to Tier 1. The result means the better reputation, the higher a.grad.rate. Also, I use four different colors, red, yellow, green and blue to represent Tier1, Tier2, Tier3 and Tier4, respectively.
The reason I choose these four colors is based the color identification ability of human visual system. Since light with a single color is a mixture of energies at different wavelengths in the visible spectrum ranging from about 380 nanometers to 770 nanometers. The variation in the amounts of radiation at the different wavelengths accounts for our different perceptions. While just three numbers that are derivable from the radiation amounts can describe our perception of color accurately, here I use HSL and HSV system to choose the best colors.
HSL and HSV are the two most common cylindrical-coordinate representations of points in an RGB color model. HSL stands for hue, saturation, and lightness. HSV stands for hue, saturation, and value (or brightness). Hue is measured in degrees from to since there is a circularity to our perception of hue. Lightness refers to how light or dark a color appears. Saturation refers to how pale or deep a color appears.
From the following picture, we can see that the angle around the central vertical axis corresponds to “hue”, the distance from the axis corresponds to “saturation”, and the distance along the axis corresponds to “lightness”, “value” or “brightness”. Note that while “hue” in HSL and HSV refers to the same attribute, their definitions of “saturation” differ dramatically.
From above picture, HSL and HSV are both cylindrical geometries, with hue, their angular dimension, starting at the red primary at 0°, passing through the green primary at 120° and the blue primary at 240°, and then wrapping back to red at 360°.
In both geometries, the additive primary and secondary colors are red, yellow, green, cyan, blue, and magenta. As showed below:
In this case, I prefer to choose three primary colors-red, green and blue at first. If additional color needed, I will pick one of these secondary colors, such as yellow, orange, and purple and so on. These colors have clear boundaries between adjacent ones, which will help viewers to identify different groups or tiers. Therefore, I choose red, yellow, green and blue to represent Tier1, Tier2, Tier3, and Tier4, and provide efficient visual assembly of the four categories, allowing us to see each category of elements as a whole, mentally filtering out the other categories.
Also construct a coplot for the same two variables where you are conditioning on Tier group.
The panel at the top is the given panel, which is tier; the panels below are the dependence panels, which are Reputation (horizontal) against a.grad.rate (vertical). Each rectangle on the given panel specifies an interval of tiers. On a corresponding dependence panel, a.grad.rate is graphed against Reputation for those observations whose values of tier lie in the interval; a loess curve has been added to the panel, which produces smoothed values at any desired collection of values along the x scale and summarizes how y depends on x. If we start at the (1,1) dependence panel, the leftmost panel in the bottom row, and move form left to right in the row, then from left to right in the next row, and so forth, the corresponding intervals of the given panel proceed from left to right and from bottom to top in the same fashion.
For the four tier intervals, the patterns on the corresponding dependence panel are somehow different. The conditioning on tier has a linear pattern(if not too picky). For the (1,1) panel on the corresponding dependence, reputation ranges from 3.0 to 5.0 and a.grad.rate ranges from 0.7 to 1.0, although from reputation 3.0 to reputation 3.5, it seems a close to flat slope, we can still treat the whole interval as a positive linear relationship. For the (1,2) panel, the reputation ranges from 2.5 to 4.0 and the a.grad.rate ranges from 0.4 to 0.8, the overall trend is an almost flat. For the (2,1) panel, the reputation ranges from 1.8 to 3.3 and the a.grad.rate ranges from 0.3 to 0.7, the overall trend is almost flat line. For the (2,2) panel, the reputation ranges from 1.8 to 2.9 and the a.grad.rate ranges from 0.15 to 0.6, the overall trend is still almost an flat line.
Compared to the Coplot, I prefer the single scatterplot with colored labels. Because color is a powerful tool for encoding data, it genuinely enhances the visual decoding of information from data displays and makes the visual operation of assembly as efficient as possible. In the Coplot, the intervals of tiers are somehow overlapped (based on the method used). For this question, I choose red, yellow, green and blue to represent Tier1, Tier2, Tier3, and Tier4, and provide efficient visual assembly of the four categories, allowing us to see each category of elements as a whole, mentally filtering out the other categories. In the colored scatterplot, four different categories of plotting symbols are color encoded, and we can easily assemble the symbols of each category. Therefore, I prefer the colored scatterplot.
Part B:
The question simulates a sample of size 100 from a bivariate normal distribution with correlation rho = -0.9 and use a bivariate density estimation algorithm to construct a contour graph of the density estimate. Colors of red, blue, green, orange, yellow, and brown are used to color the regions of the contour graph.
As we can see the original graph use red, blue, green, orange, yellow and brown to represent 0.05,0.1,0.15,0.2,0.25 and 0.3.(all the value are random)
The improved graph:
Based on the two desiderata in choosing a color encoding of the quantitative values of a function. First, we want effortless perception of the order of the values. Second, we also want clearly perceived boundaries between adjacent levels. The original graph just satisfied the second desiderata. However, those colors just make people easy to identify the differences but hard to see the order of the values. The improved graph is a color level plot , which encodes different level regions by different colors. The level region for the levels is the set of (u,v) values in the plane whose function values lie in the level interval and a level is an interval of values along the measurement scale of a function. It provides effective visual efficient visual assembly of the six categories, allowing us to see each category of elements as a whole. There are 6 intervals, ranging from the minimum to the maximum function values. There are two hues, cyan and magenta. From the middle to the extremes, the cyan ranges from 30%-cyan to 100%-cyan in steps of 33%-cyan, corresponding to 0.15 to 0.05. And the magenta ranges from 30%-magenta to 100%-magenta in steps of 33%-magenta, corresponding to 0.15 to 0.30. This method provides efficient ranking because it allows accurate ordering and it allows a sufficient number of distinct colors. Therefore, this improved graph gives a good compromise to both goals, effortless perception of the order of the encoded quantities and clearly perceived boundaries between adjacent levels. Also,it genuinely enhances the visual decoding of information from data displays.
The dataset UScereal in the MASS package gives eleven variables for a group of 65 breakfast cereals. Based on the requirement I choose three variables, which are calories, fat and potassium. Later, I construct a scatterplot matrix, a coplot and a spinning 3-dimensional scatterplot for these variables.
The first graph is a scatterplot matrix with variables calories, fat and potassium.
Scatterplot matrix is a method for studying multidimensional data. It sample, elegant solution to a difficult problem is one of the best graphical ideas around for displaying scattered measurements of three of more variables. As we observed, each panel of the matrix is a scatterplot of one variable against another. The upper right triangle of the scatterplot matrix has all of the pairs of scatterplots, so does the lower left triangle. For example, in my graph the (2,1) panel is a graph of potassium on the vertical scale against fat on the horizontal scale, and the (3,2) panel has the same variables but with the scales interchanged.
According to above graph, we can see that the calories and fat, calories and potassium, and fat and potassium all have positive relationship with each other. The overall trend is, as fat increases calories will increase, as potassium increases fat will increase too, and as potassium increases calories will increase as well, and vice versa. (If not too picky for the overall trend)
Specifically, for the upper right triangle of the scatterplot matrix, saying the (2,3) panel (calories vs. fat), we can divide it into 3 parts. The first part, calories has a decrease until fat increase to almost 1 gram. After 1 gram of fat, which is the second part, calories have a positive relationship with fat, until fat increase to 1.5 grams. After fat increases more than 1.5 grams, calories and fat almost have a comparably smooth positive linear relationship.
For the (3,2) panel (fat vs. potassium), we can divide it into 3 parts. The first part(most points locate in this area), fat increases until potassium increases to almost 200 grams. After 200 grams of potassium, which is the second part, fat almost keeps constant until potassium increases to 400 grams. After potassium is greater than 400 grams, which is the third part, fat keeps a positive linear relationship with potassium.
For the (3,3) panel (calories vs. potassium), we can divide it into 2 parts. The first part(most of points locate in this area), calories increase until potassium increases to 400 grams. After 400 grams of potassium, which is the second part, calories have a close to flat positive slope with potassium.
For the lower left triangle, including (1,1), (1,2), (2,1) panels, we get the similar conclusion that calories, fat, and potassium have positive relationship with each other.
The display method of the coplot presents conditional dependence in a visually efficient way. The panel at the top is the given panel, which is potassium; the panels below are the dependence panels, which are fat (horizontal) against calories (vertical). Each rectangle on the given panel specifies an interval of values of grams of potassium. On a corresponding dependence panel, calories is graphed against fat for those observations whose values of potassium lie in the interval; a loess curve has been added to the panel, which produces smoothed values at any desired collection of values along the x scale and summarizes how y depends on x. If we start at the (1,1) dependence panel, the leftmost panel in the bottom row, and move form left to right in the row, then from left to right in the next row, and so forth, the corresponding intervals of the given panel proceed from left to right and from bottom to top in the same fashion.
For the first four-potassium interval, the patterns on the corresponding dependence panel are similar (if not too picky). The conditioning on potassium has a nonlinear pattern: a slight hockey-stick function. For the (1,1), (1,2), (1,3), and (2,1) panels on the corresponding dependence, the range of fat is within (0,200) grams and the range of calories is within (80,200). For example, for the leftmost panel on the first row, below 1-gram fat, the pattern is negative linear; above this value, it is a nonlinear positive line. Similar relationship happens in middle panel of bottom row and leftmost panel of upper row. The relationship between calories and fat on the rightmost panel on the bottom row is a little bit complicated. Specifically, we can divide it into 4 parts. The first part, calories increase until fat increases to almost 1 gram. After 1 gram of fat, which is the second part, calories take a sharp increase until fat increases to 2 grams. When fat is greater than 2 grams but less than 3 grams, which is the third part, calories a negative linear relationship with fat. After fat is greater than 3 grams, calories have a close to flat positive slope with fat.
For the last two-potassium intervals, the patterns on the corresponding dependence panel are just simply positive linear relationship between calories and fat. However, due to the three variables that I choose, the last interval is longer than any of other intervals, which range (0,9) grams of fat and range (100,400) calories.
From the above 3-dimensional scatterplot, we can see that the calories and fat, calories and potassium, and fat and potassium all have positive relationship with each other. The overall trend is, as fat increases calories will increase, as potassium increases fat will increase too, and as potassium increases calories will increase as well, and vice versa. Here’s also a video that shows spinning the plot by use of the mouse. I think the spinning feature is really necessary to see the 3-d structure in the graph.
Finally, I find two “special” cereals that seem to deviate from the general relationship patterns. They are listed following:
# calories fat potassium
# Grape-Nuts 440.00000 0.0000000 360.00000
# All-Bran with Extra Fiber 100.00000 0.0000000 660.00000
For Grape-Nuts cereal, which has the highest calories and comparably high potassium but no fat, these features deviate from the general relationship patterns that as calories increases fat will increase, as potassium increases fat will increase too. In the scatterplot matrix, we can find this point (red) deviates from the overall pattern in (1,2),(2,3) panels, located at either upper right corner or bottom right corner.
The other special cereal is All-Bran with Extra Fiber, which has the third highest potassium but with low calories and no fat. These features deviate from the general relationship patterns that as potassium increases calories will increase, and as potassium increases fat will increase too. In the scatterplot matrix, we can find this point (red) deviates from the overall pattern in (1,1), (1,2), (3,3) panels, located either upper left hand side or lower right hand side, away from other points.
As required, I choose one time series data set in the “datasets” package, which is sunspot.year. This data set is yearly sunspots data from 1700 to 1988. Then, I use all four methods to graph the data and explain which method is best for your dataset.
From the allowing graphs, we can see an overall trend of sunspot from 1700 to 1988. Interestingly, the sunspots do not show an obviously increase in their overall level. Only in 1957 and 1958, the total number of sunspots is over 180.In addition, the graphs also shows the sunspot has cycles with an average period of about 11 years. It is good to know that increased sunspots are associated with increased solar activity, such as solar wind. For people who are major in geophysics, maybe this interesting result can be explained by a professional way.
The first graph is connected symbol plot, which is symbols together with lines connecting successive points are used. The connected symbol plot allows us to see the individual data points and the ordering through time. A connected symbol plot is appropriate when we want to see the individual data points and the ordering through time. The connected plot the individual data points are not unambiguously portrayed, and each point is clearly seen by readers (For instance, each peak is consists of one value, we don’t need to doubt whether the peak is a single outlier or is supported by a rise and fall of few values). For example, we not only see the each individual point, but also an 11-year cycle (approximately) and a trend from 1700 to 1988. For the sunspots example, the connected symbol plot seems provide the best portrayal.
The second graph is symbol plot, which is just the symbols are used, which cannot perceive the order of the series over short time periods of several years. A symbol plot is appropriate if we want to study the long-term trend, that is the low frequency behavior. In such a case it is not necessary to perceive the exact time order over short time intervals. However, the symbol plot does not give a clear portrayal of the 11-year cycles because we cannot perceive the order of the series over short time periods of several years. For the sunspots high frequency behavior, symbol plot is obviously not a good choice.
The third graph is a connected plot, which is just the lines are used. A connected plot is appropriate when the time series is smooth, so that perceiving individual values is not important. However, the sunspots data reveals a fluctuate situation, instead of smooth. Moreover, to avoid ambiguity, we’d better know which peak is a single outlier and which peak is supported by a rise and fall of few values. In this case, each individual point is important for graph interpretation. Therefore, I think connected plot is not a good choice too.
The fourth graph is a vertical line plot, which is just using the vertical line to represent each year’s response value. A vertical line plot is appropriate when it is important to see individual values, when we need to see short-term fluctuations, and when the time series has a large number of values. The use of vertical lines allows us to pack the series tightly along the horizontal scale. Moreover, the vertical line plot usually works best when the vertical lines emanate from a horizontal line through the center of the data and when there are no long-term trends in the data. However, there may be a disconcerting visual phenomenon, which means human visual system cannot simultaneously perceive the peaks and the troughs. On this sunspots example, there is an unfortunate asymmetry. The vertical line plot the peaks stand out more clearly than the troughs. Hence, I will not pick the vertical line plot as the best one.
In sum, after comparing the above four graphical methods, I think connected symbol plot method of graphing a time series provides the best portrayal. Since a connected symbol plot is appropriate when we want to see the individual data points and the ordering through time, it gives readers the most information it could. The connected symbol plot not only provides the each individual point, but also an 11-year cycle (approximately) and a trend from 1700 to 1988.
Loess
First, simulates some (x, y) data where the true signal follows one of the curves sin(x)+cos(x), sin(x)-cos(x), sin(x)*cos(x), .28-.88*x-0.03*x^2+.14*x^3.
Then we get a list, where d$x is the x values and d$y contains the y values.
> head(cbind(d$x,d$y))
[,1] [,2]
[1,] -3.141593 -0.7723653
[2,] -3.110019 -1.0347078
[3,] -3.078445 -1.3321508
[4,] -3.046871 -1.9027887
[5,] -3.015297 -1.4537965
[6,] -2.983724 -1.9512365
Using the simulated data …
1. Construct a scatterplot of your data and overlay a lowess smooth (using the default value of f in the lowess function).
Loess produces smoothed values at any desired collection of values along the x scale and summarizes how y depends on x. From the above graph, we can see that there is nonlinear relationship between x and y. An increase in Y as x increases until x is close to 1,saying a positive relationship between x and y and the effect is nearly linear and the slope is close to 1. From 1 and above, the an decrease in Y as x increases until x is close to 3,saying a negative relationship between x and y and the effect is nearly linear and the slope is close to -1.(The whole graph is definitely nonlinear, just for better explanation, I divided the graph into two parts, each part seems linear relationship between x and y. )
2. Construct a plot of residuals and comment if the lowess curve has effectively found the signal.
There is a fluctuant pattern in the residual graph, the problem is that the loess smoothing in the top panel has missed part of the pattern because is too large, and this missed part has gone into the residuals. In this case, we should reduce value, (For example, drop from default alpha to alpha=0.25 ), Although the amount of smoothing for the curve may be not great, the loess curve on the residual will be reasonable close to a horizontal line, which suggests the loess curve with is not distorting the underlying pattern in the data.
Then I combine two graphs in one for better visual effect:
By combining two graph together, we can see clearly both relationships of y and x and residuals and x, with the same horizontal scale.
3. Assuming that a better smooth can be found, construct a scatterplot using a better choice of f. By the use of a residual plot, demonstrate that your choice of f is better than the default choice in 1.
Since the default f yields certain pattern in residuals, which means alphais too big, I reduce the alpha value from default to 0.25 eventually. First I tried alpha=0.5, however the loess curve on the residual graph still shows a fluctuated pattern, then I continuous drop alpha value from 0.5 to 0.4, 0.3, 0.25, until the loess curve on the residual graph is nearly a horizontal line since the residuals should be variation in y not explainable by x. Meanwhile, to keep alpha from being too small is to increase it to point where the residual graph just begins to show a pattern, and then use a slightly smaller value of . In this case, we can either avoid the loess curve on the residual has a pattern, or keep from being too small. As saying above, I end up with using alpha=0.25, which make the loess curve on the residual graph is nearly a horizontal line.
To demonstrate the whole procesure, I first upload a graph with alpha=0.5, which makes the residuals vs. X still has a certain pattern. 
From this graph, we can see that f=0.5 is not the best choice, since the fluctuated pattern still exist. Then I continuous reduce f value until the loess curve on the residual graph is nearly a horizontal line, with f=0.25.
As we see in the above graph, comparing to the default value alpha=2/3, which has obvious fluctuate pattern in residual, the loess curve on the residual graph is nearly a horizontal line and the residual graph has no certain pattern, with f=0.25, which means the residuals is variation in y not explainable by x.
Also there is a new scatterplot of x and y, using a better choice of f.
From the above graph, we can see that there is nonlinear relationship between x and y. An increase in Y as x increases until x is close to 1, the response is in fact constant until x=-2 and then the response increase as x increases until x=1. From 1 and above, the an decrease in Y as x increases until x is close to 3,saying a negative relationship between x and y. Comparing the first graph using default f, this lowess smooth explain the data better, telling us more detail information from the graph.
Finally, for better visual effect, I combine the scatterplot with lowess smooth and a plot of residual with lowess smooth in one graph. From the following graph, we can see that with the residual graph has no certain pattern, the scatterplot with lowess smooth could explain the original data better.Comparing to the default value(alpha=2/3), alpha=0.25 yield better lowess smooth. Also,by combining two graph together, we can see clearly both relationships of y and x and residuals and x, with the same horizontal scale.
Find a two-way table (this is a table with a response, like temperature, and row and column classifications, like city and month).
The table should have at least 4 rows and at least 4 columns. According to this requirement, I collect data from Ohio Department of Education: http://ilrc.ode.state.oh.us/power_users.asp
Data is regard to high school graduate number in different school district in Ohio.
Construct three dotplots.
1. Find the mean response for each row. Construct a dotplot of the means where the means are ordered from high to low.
My data’s row is school district, column is year, response is high school graduate number.
Answer: Figure 1 is the average high school graduate count (# of people) in 5 years (from 2006 to 2010) for 5 Ohio school districts, which are Archbold-Area Local, Ansonia Local, Alliance City, Alexander Local, and Adams County. Since my data is ordered from high to low by row (School District), the distribution of the average high school graduate count of 5 school districts is clearly showed in above graph. We can see that the school district “Adams County” has the highest 5-year average high school graduate number, which is close to 300. We can interpret that this school area either has a large population, or the reputation in this school area is very good, which attract many students to enroll in. Also, the school district “Ansonia Local” has the smallest 5-year average high school graduate number, which is barely above 50. We may interpret that this area has less population than other school districts. After Google this county, I found it located close to the bounder of Ohio and Indiana, quite a remote place and no surprise it has less high school graduates (only has one high school in this school district).
Moreover, the order of the categories for each categorical variable is an important aspect of the dot plot display method that substantially affects our visual decoding. The ordered data graph is more informative than non-ordered one. On one hand, when we study a distribution of values such as the high school graduate in different school districts, we want to know what is large, what is medium, and what is small. The organization in ordered data graph allows us to easily assemble and estimate the large values, or the medium values, or the small values. On the other hand, we cannot do this nearly as effectively in non-ordered data graph, because each of these sets of vales is scattered throughout the graph.
2. Construct a dotplot, grouping by rows.
Answer: Figure 2 showed above is a multiday dot plot, grouped by rows, which are School Districts here. The high school graduate data are now graphed with a single school district on each panel. Now we can more effectively decode information about time trend for each school district. Corresponding to Figure 1, Adams County has the highest high school graduate number each year, form 2006 to 2010, among the five school districts. Ansonia local has the smallest high school graduate each year. Also for each school district, the distributions of graduate are not same. For instance, Ansonia local seems keep the same graduate number for the past 5 years, only 2006 has several more. For Adams County, the distribution is quite fluctuated. In 2008, it has the lowest graduate number, which is only 250, much lower than its average graduate number, and 2010 has the highest graduate number, which is greater than 300. For Archbold-Area Local and Alliance City, the shape is quite similar, like an arrow, both districts have the highest graduate number in 2008. However, Archbold-Area Local has an even less graduate number in 2010 than in 2006. For Alexander local, the high school graduate number is quite stable, but still have lowest graduate number in 2008, though the difference is not big.
3. Construct a dotplot, grouping by columns.
Answer: Figure 3 showed above is a multiday dot plot, grouped by columns, which are Year here. The high school graduate data are now graphed with a single year on each panel. Now we can more effectively decode information of 5 school districts for each year. Corresponding to Figure 1, Adams County always has the highest high school graduate number for 5 year, form 2006 to 2010, among the five school districts. Ansonia local has the smallest high school graduate each year. Five panels have similar pattern. For these 5 panels, Adams County has the highest graduate number, next is Alliance City, the smallest graduate number is Ansonia Local in all 5 years. However, in 2007 and 2008, Archbold-Area Local has higher graduate number than Alexander Local. In the rest years, 2006,2009,2010, Alexander Local has higher graduate number than Archbold-Area Local. This is the only difference for the 5 panels’ pattern.
I think to group the data by rows or by column is depend on need. If you want study each school district’s high school graduate situation, it is better to group the data by rows, here means by school district. In this way, it is more effectively decode information about time trend for each school district. However, if you mainly want to compare these five school districts’ graduate number each year, it is better to group the data by columns, here means by year. In this way, we can easily compare different school district year by year, and know which district has the highest graduates, which has the smallest graduates. However, this way may hamper us to see a single district’s trend.
For this school district graduate data, I prefer to group data by rows, here means by school district. Since I have already draw the dot plot the average high school graduate count (# of people) in 5 years for 5 school district in Figure 1, from which I have already know overall comparison for 5 districts. I would like to get more information about each of these school districts. In this case, grouping by school district is best for my interest.
As required in the instruction, I find the data set, remove all the missing data, and randomly pick 1oo sample from the above data set. Since my first name’s first letter is between A to J, I look at the haircut prices of the men and women in the class. (The relevant variables in the data frame are Haircut and Gender.)
1. Construct parallel stripcharts of the variable by gender.
From the parallel stripchart we can compare the distribution of two groups of students and see that male students’haircut prices have narrow range, which is from 0 to 25 dollars. However, female students’ haircut prices have very wide range, which is from 0 to 145.On one hand, there are one third of male students(11) do not spend any money on haircut and almost half of male students(16) spend from $10 to $15, and only two male students spend more than $20 on haircut. The maximum money spend spends on haircut for male student is $25. On the other hand, over two third (47) of female students spend from $10 to $50 on haircut. Three females do not spend any money on haircut and only 4 female students spend more than $100. The maximum money spends on haircut for female student is $146. The distributions of these two groups are quite different.
2.Construct parallel quantile plots of the male values and of the female values. Write several sentences that help the reader interpret the quantile plots.
From the graph below we can see that the first quartile of male student is $0 , median quartile of male is about $10 and upper quartile is about $15. However, first quartile of female student is about $10, the median quartile of female is about $30 and upper quartile is about $50. Comparing these two groups, we are clear that female students spend more than male students on haircut, no matter for the first quartile or the medium quartile of people. Moreover, the median quartile of female student to have a haircut is more than the upper quartile of male student.
3.Construct a quantile-quantile plot of the male and female values.
From the first graph we can see that the average female student haircut price is obviously higher than male student (the slope of the line is obviously greater than 1). However, the “extra price” is not constant. We have to observe the graph in different segments. If the male student haircut price is within the low price region, saying $0-$10, female haircut price is about $10 higher. However, if the male student haircut price is more than $10, female haircut price will increase faster than the low price region. For the high price region (for male haircut), say $10-$24, for every one dollar more increase for male haircut, female haircut price will increase 5 dollar more (from $25 to $90). For the high price region (for male haircut), saying $25 and more, female price increase rapidly, ranging from $110 to $145. Meanwhile, there are also points located at y=x line, which means several female spend nothing as male spend.
4. Construct a Tukey m-d plot from the quantiles of the two samples. Interpret the plot. Is there a simple relationship between the male values and the female values?
For the mean price between $0 and $20, the difference has a range from $0 to $20 and the difference rise and fall, quite fluctuating. For the mean price more than $20, the differences continue growing, with a slope almost equal to 1.5. The graph also indicates that the biggest difference is about $120 and the smallest difference is $0. There are no simple relationship between male haircut price and female haircut price.
In sum, for the mean price within $0 to $20, the difference is quite fluctuating. However, for the mean price over $20, it seems we can interpret the line as linear relationship, y=-10+1.5x (y is the price difference and x is the mean price.) Female haircut price is always expansive than male haircut price, except those haircut by themselves, relatives or friends with no charge. This conclusion is easy to understand. For simple haircut at a small hair salon, the price difference is not that big. However, if a female want to have a perm or color hair at a high class salon, the price will surely high. Meanwhile, males do not tend to decorate their hair as females, so they spend less than female.
Exploring the Pythagorean Formula
collect for a number of teams, the following variables:
W – the number of games won
L – the number of games lost
P – the number of points (or runs, goals, etc) scored by the team
PA – the number of points allowed by the team
Then the Pythagorean formula (described first by Bill James in the context of baseball) says that
W/L= (P/PA)^k
where k is a constant that is dependent on the particular sport.
Taking logs, we can reexpress this formula as
Log(W/L)=k*Log(P/PA)
First, I collect this type of data for 2012-2013 NBA season data from http://nba.sports.sina.com.cn/league_order1.php. For the data, which includes number of games won and number of games loss, and also average points scored and allowed for 12 NBA teams, which are Heat, Knicks, Net, Bulls, Hawks, Pistons, Bucks, 76s, Magic, Bobcats and so on.
Secondly, construct a scatterplot of log(W/L) against log(P/PA) and overlay the best fitting line of the form k log (P/PA). The red line is the least-squares fit with the k equal to 14.52165. The blue line is a lowess line, which uses locally-weighted polynomial regression. Then I construct a plot of the residuals against log(P/PA) at bottom panels as the graph shows.
To get k, I use R, the output is following:
> k=lm(log2(W/L)~log2(P/PA))
> summary(k)
Call:
lm(formula = log2(W/L) ~ log2(P/PA))
Residuals:
Min 1Q Median 3Q Max
-0.34265 -0.19283 0.01339 0.19698 0.34505
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.03939 0.07181 0.549 0.595
log2(P/PA) 14.52165 1.15496 12.573 1.88e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
According to my graph, we can see that these 12 teams residuals are quite randomly plotted. These residuals
stay within a range of (-0.02, 0.02), New York Knicks has residual almost at 0 and the rest of teams are all
around the abline=0. Also, from the upper panel, we can see that most of teams are around the regression line.
Each point represent a team’s ratio of Log(Win/Loss)/log(Points scored/allowed). Since the positive
relationship,we may say that the team with higher win/loss ratio tends to have higher points scored/allowed ratio.
Obviously, Miami Heat is the best team in league now（as the graph shows). Heat has the highest win/loss ratio,
and also has the highest points scored/allowed ratio. Meanwhile, Bobcats, with only 12 win and 40 loss, is not that
good in this season with the lowest win/loss ratio and lowest points scored/allowed ratio. In addition, you may pay
attention to the highest point and the second high point, there is a quite a gap between Heat and Knicks. I have to say
that to catch up with Heat, Knicks has to try hard in next season.
Which Log?
Collect some measurement that has changed exponentially over time. (You should have at least 10 measurements.)
According to this requirement I collect data from world dataBank, World Development Indicators(WDI), the link is http://databank.worldbank.org/ddp/home.do
In this blog, I construct two graph. first one is a display with log base 10 measurement against time and the second one is a display with log base 2 measurement against time. In the following two graph you will see both graphes have log measurement on left vertical scale and actual value on the right vertical scale.
The first graph is with measurement in log10, which has a range from 2.75 to 3.5 on the left vertical scale. However, the second graph is with measurement in log2, which has a range from 9.00 to 12.00 on the left vertical scale. By the nature of Logarithms method, different base does not change the pattern of points but changes only the values at the tick marks because the logarithm of one base is just a constant times the logarithm of another base. The overall trend of this graph is that the GDP of China keep growing as time goes by from 1992 to 2011. Also, the line segments connecting successive plotting symbols are banked to 45 degree in both graphs.
The choice of the base depends on the range of the data values that need to be visually compared. Since my original value has measurement unit in “Billion” , the largest data only has 3 powers of 10 and the smallest data has 2 powers of 10. In this case, it is inevitable that equally spaced tick marks for log base 10 will involve small fractional powers of 10, as my first graph showed. It is difficult to deal with such fractional powers. In this situation, it is reasonable to convert to log base 2 as the second graph showed. Although the second graph has fractions as well, they are comparably small to the fraction in the first graph. It is easier to deal with powers of 2 than small fractional powers of 1o. Moreover, both graphes has been processed by “statistical scientist’s trick”, which take the original units to be in billion. For log base 2, the original data will make the scale range from 19.0 to 21.5. However, now it only range from 9 to 12.5.
In sum, I think the second graph with log 2 base is the best choice. The principle of choosing log 2 or log 10 is based on the situation and visual comparison. When the data range though two or fewer powers of 10, the log base 10 scale is not as informative since we must deal with fractional powers of 10. When data go through a small number of powers of 10, log base 2 often provides a useful scale, as I showed in the bottom graph.
I collect the population of another country, Guatemala, for the same ten-year period that I used in the previous blog two scales. After data collection, I compare the log (base 2) population against year for the two countries, Honduras and Guatemala. Here, I use one panel and two connected curve to display these two countries’ population.
From the graph we can see that the population of Guatemala is higher than Honduras for the past ten years.However, the growth rate is almost same in two countries. In this graph,red triangle represents Guatemala,and pink cross circle represents Honduras.
Interesting part in this graph making:
1. How to draw legend outside of the plot dimension? How to correctly use command “legend”?
2. What kind of margin ratio is best for graph making?
The website http://data.worldbank.org/indicator/SP.POP.TOTL?cid=GPD_1 gives the population of many countries for many years.
I collect population data for Honduras from 2002 to 2011,and graph the log (base 2) of the population against year. Construct two scales for your graph where the left vertical scale shows the log (base 2) population and the right vertical scale shows the population.
From the graph, we can see that the population in Honduras is keeping growth for the past ten years, from 2002 to 2011. The the unit of measurement on the right vertical scale is in million and the left log population (base 2) is also in million measurement unit. However, it does not look like exponential.
Interesting part in this graph making:
1.The R help gives us par(mar=par()$mar+c(0,0,0,3)), is that equivalent to par(mar=c(5.1,4.1,4.1,5.1))? Why we will use the “+” in this commend?
2. To limited the decimal, I use the command “format(round(2^seq(2.7,3.0,0.05), 2), nsmall = 2)”
3. what is the best way to add tick mark label on every tick mark? I used the following code:
d <- seq(2.70,3.0,by=0.05) plot(Year, log2(Popu), pch=19,ylab="log2(Millions)",yaxt = 'n') axis (2, at= d)
The dataset UScereal in the R MASS library gives nutritional information for a selection of US cereals.
Find two variables in this dataset that are associated and use the plot function in R to draw a scatterplot. In this case, I decided to use two variables, “Fat” and “Calories”, to draw a scatterplot. Later I redraw this graph, violating two of the attributes of Clear Vision described in Chapter 2. Here we can see these two graphs below:
Comparing these two graphs, we can see that the upper one has a clear vision, which will help readers better understanding the data. However, the lower one has an unclear vision of the same graph.
Firstly, the second graph violates the principle that “Overlapping plotting symbols must be visually distinguishable”. because of exact and near overlap, some of the data cannot be seen. Also, because of this particular choice of plotting symbols, solid circle, it is hard to see an exact or close point. The advantage of using default choice is that it is clearer than filled squares when the data are close to each other. We can see clearly two closed and overlapped unfilled circles, but blurry two filled squares. Because the solid portions of the symbols can form uninterpretable blobs, it is hard for people to distinguish.
Secondly, the lower one violates the other principle that “Do not allow data labels in the interior of the scale-line rectangle to interfere with the quantitative data or to clutter the graph”. On the second graph, the data labels interfere with our visual assembly of the plotting symbols. The labels and points mix together. The result is that the labels camouflage the point cloud. The problem of the data labels is the word font-size is too big and they are too crowded.
Lastly, the lower one violates the principle that “Visual clarity must be preserved under reduction and reproduction”. In this graph, we almost can see a shadow small letter behind the front big letter. The shading is barely visible due to poor reproduction. In addition, a good graph should make the sequence of graphs and their captions as nearly independent as possible. The lower one’s graph and caption may be too close to each other.
Some question in R
1. Since R’s default format, it is easy to draw a graph with only two sides of scale lines. However, I tried several ways but just couldn’t draw a pair of scale lines for each variable. Anyone knows this code? Thanks
2. How to draw a graph with the data rectangle as the same size as the scale-line rectangle? and how to make tick marks inside ward ?
This is the final graph that I get from R. From the graph we can see that the tuition fee keeps increasing from 1960 to 2000. It looks like that the year and tuition fee have a positive relationship. We can expect the tuition will continue growing in the future based on the current graph.
1: In simpleLoess(y, x, w, span, degree, FALSE, FALSE, normalize = FALSE, : pseudoinverse used at 1980...
quartz(width=10, height=8, pointsize=18,canvas="peachpuff")
par(oma=c(4,4,4,4))
with(tuition1, plot(tuition1$Year,tuition1$Log10Fees,main="Tuition growth",cex=1.2,
xlab="Year",ylab="Log10 of Fees", type="b",pch=19))
abline(v=2011,col="deepskyblue3")
text(2011, 3, label=c("I started college at BGSU since 2011"),cex=0.5,srt=90)
mtext("The instructional fees (per term) for BGSU for selected years.
From the graph we can see that tuition fee keeps increasing from 1960 to 2000.
The tuition and the log10fees look like have a positive monotonous relationship.
Moreover, it can be expected that the tuition fee will continue growing in the future based on current graph.",
outer=TRUE, cex=0.5, col="firebrick", side=3, lwd=3)
Welcome to blogs.bgsu.edu This is your first post. Edit or delete it, then start blogging!
Motor Trend magazine collected the horsepower and mileage for 32 cars in the 1973-74 model year. To see if there is any relationship between horsepower and mileage, I construct a scatterplot of the these two variables, Horsepower and Mileage.
From the Graph,we can see that Mileage decreases as the Horsepower increases. The Mileage and Horsepower have a negative relationship, though not a linear negative relationship. It can be seen clearly that Mileage drop tremendously when the Horsepower increase from 50hp to 150hp.When the Horsepower stays at 180hp, the Mileage seems range from 15mpg to 20mpg. However, there are extreme values of Mileage at 10mpg when the Horsepower ranges from 200hp to 220hp. After the Horsepower goes beyond 250hp, the Mileage increases to 15mpg and stays around 15mpg as the Horsepower increases up to more than 300hp.