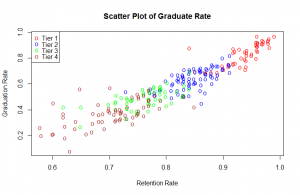
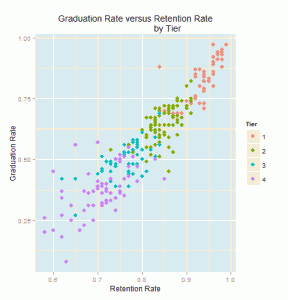
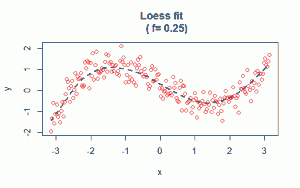
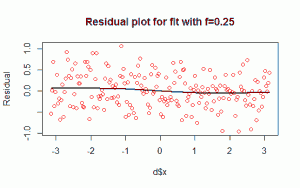
In this blog I have used three different types of graphics such as stripplot, Parallel Quantile plot , Quantile-Qunatile plot and Tukey m-d plot for male and female students’ height collected in an introductory statistics class to see the difference in the distribution of the height of male and female students.
In the original dataset there are many variables, of which I have selected two variables –Gender and Height. A random sample of size 100 is then finally selected from the large dataset.
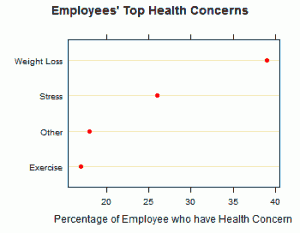
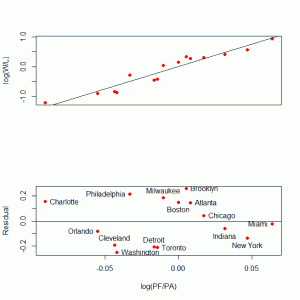
The stripplots show that male students’ height is more than female students’ height.

This above figure shows parallel quantile plots of the distributions of the heights of male and female students. The median height of female students is about 65 . On the other hand, the median height of male students is 70.

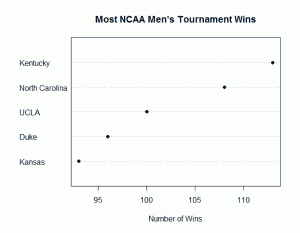
In the left panel quantiles of female students’ height are graphed against corresponding quantiles of male student’s height. In the entire range of the distribution, the male students’ height is greater than that of female students’ height. There is no simple relationship between male and female students’ height.
In the right panel Tukey mean difference plot is drawn. It shows that all male student’s height is higher than that of female students except one . It is very hard to find exact comparison between two groups.
R code:
library(lattice)
library(ggplot2)
d=read.table("http://bayes.bgsu.edu/eda/data/studentdata.txt",header=TRUE,sep="\t")
d.complete=d[complete.cases(d),]
d.sample=d.complete[sample(559,100),]
d.data=subset(d.sample,select=c(Gender,Height))
#####################################
stripplot(Height~Gender,data=d.data)
######################################
d.male<-subset(d.data,Gender=="male")
attach(d.male)
d.male.s<-d.male[order(Height),]
detach(d.male)
d.male.final<-within(d.male.s,{
id=seq(1,nrow(d.male.s))
f<-(id-0.5)/nrow(d.male.s)
})
d.male.final
d.female<-subset(d.data,Gender=="female")
attach(d.female)
d.female.s<-d.female[order(Height),]
detach(d.female)
d.female.final<-within(d.female.s,{
id=seq(1,nrow(d.female.s))
f<-(id-0.5)/nrow(d.female.s)
})
d.female.final
data.final<-rbind(d.male.final,d.female.final)
data.final
p <- ggplot(data.final, aes(f, Height)) + geom_point()
p + facet_grid(. ~ Gender)
#p=ggplot(d, aes(Haircut, Gender))
#p + geom_point(position = position_jitter(h=.1))
###########################################
d.male1<-subset(d.data,Gender=="male")
d.female1<-subset(d.data,Gender=="female")
d.female2=d.female1[sample(64,36),]
dd2<-rbind(d.male1,d.female2)
dd2
#p <- ggplot(mpg, aes(displ, hwy))
#p+geom_point()
#d.data=subset(d.sample,select=c(Gender,Height))
library(lattice)
#windows(height=10, width=10)
#par(mfrow=c(2,2))
plot1<-qq(~Height|Gender,data=dd2,
aspect=1))
attach(dd2)
dd3<-unstack(Height,Height~Gender)
dd3<-within(dd3,{
Mean<-(male+female)/2
Difference<-(male-female)
})
plot2<-xyplot(Difference~Mean,aspect=1,data=dd3)
#with(dd3,plot(Difference~Mean, col=2, pch=19))
print(plot1,position=c(0,0,.5,1),more=T)
print(plot2,position=c(0.5,0,1,1))
#par(mfrow=c(1,1))
#xyplot(Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
# data = iris, scales = "free", layout = c(2, 2),
# auto.key = list(x = .6, y = .7, corner = c(0, 0)))
#qq(voice.part ~ height, aspect = 1, data = singer,
# subset = (voice.part == "Tenor 1"| voice.part == "Bass 2"))
library(lattice)
plot3<-qq(Gender~Height, aspect=1,col=2, pch=19,data=d.data)
plot4<-tmd(qq(Gender~Height, aspect=1,col=2,pch=19,data=d.data))
print(plot3,position=c(0,0,.5,1),more=T)
print(plot4,position=c(0.5,0,1,1))