A crisp chill enters the air. A bowl of nachos appears atop my couch-side table. The soothing sounds of John Stirling creep into my ears. Why yes, it is October 2nd: the official start of the 2018 Major League Baseball postseason.

I have been a lifelong fan of baseball, and relatedly, a lifelong fan of baseball statistics. I am all too familiar with Bill James and his revolutionary handbook, paving the way for sabermetric-focused scouting, team-building, and analysis. One of these revolutionary formulas include the Pythagorean relationship, which explains the connection between the logarithmic ratios of both 1) wins to losses, and 2) runs scored to runs against. I couldn’t wait to begin this assignment, despite my favored Detroit Tigers not being studied.

For reference, here are two variations of the Pythagorean relationship:

And, in logarithmic form:

As one might guess, we will need to determine this value of k!

I decided to study 12 Major League Baseball teams from the 2018 season. These twelve teams were not randomly sampled; I selected the teams with the 12 best records in the majors. These twelve teams, in addition to their wins, losses, runs scored, runs against, etc., are shown in the image below. Specifically, I extracted these values from ESPN.com:

I was mostly intrigued by this year’s data because there were some noteworthy accomplishments among the top teams. First, the Boston Red Sox won an unusually large 108 games in the regular season. I was very curious to see if their ratio of runs would have been the major contributor for their success. Second, the 12th best record belongs to the Seattle Mariners, who surprisingly have a negative run differential. This seems very unusual for a team with 89 wins, and I wanted to see how extreme their residual value would be. Third, there were many teams (6 to be exact) who all had wins in the 89 to 92 range. I am excited to see how their Runs Scored/Run Allowed ratios and their residuals compare to one another.

Not that it is very important, but I included a screenshot of the Excel Workbook I used for these twelve teams. I now included some additional columns for the teams, which are Win/Loss ratio, Runs Scored/Runs Allowed ratio, and the logarithms of those values. This screenshot is shown below:

Let’s get to work!

I saved the Excel work as a CSV and read the file into R Studio. Then, I saved the information into two data frames: the first dataframe held the values for Log(W/L) and Log(RS/RA), while the second data frame held values for the residuals when compared to Log(W/L). In creating these dataframes, I had some guidance thanks to Dr. Albert (thanks again!).

First, to help determine the best value of k, I created a scatterplot comparing Log(W/L) and Log(RS/RA). It is shown below:

Before I calculated the value of k (which in this case is the slope, since k is the value of the exponent when a logarithm is not applied), I noticed that there were some observations which deviate from the best fit line. Thus I predicted that some big residuals will occur!

My calculation of k will not be perfect, but it will be relatively accurate. Two coordinates along the line I chose were (0.10, 0.05) and (0.15, 0.076). Using the formula for slope, k is calculated to be 0.52. In other words, for every unit increase in Log(W/L), the Log(RS/RA) ratio also increases by a value of 0.52.

Next, I created a Figure with R Studio similar to that of Figure 3.5 in the textbook. The top figure is the one which I discussed above. The bottom figure is a residual plot for the two ratios. This fancy little figure is shown below:

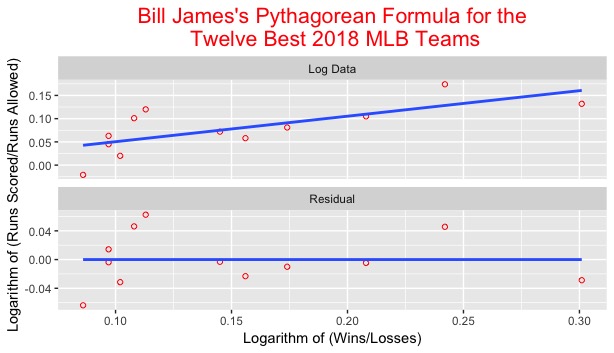
As predicted earlier, there are some big residuals here! The negative residual on the far left represents the infamous 89-win Mariners. Their residual lies so far below the residual line due to the fact that their run differential is a negative value. This affected their Log(RS/RA) ratio, as seen in the scatterplot in the top figure; their observation falls below 0 and well below the best fit line. This team is very lucky though. Despite a negative run differential and log (RS/RA) ratio, they ended up with 89 wins! That is very impressive.

One other unusual residual is the negative residual at approximately x = 0.30. Wildly, these observation belongs to our talented Red Sox team! This residual tells us that while their Win Loss ratio is large, it does not result in a proportionally large run differential or ratio. In other words, the Red Sox were expected to have a better runs ratio based on their superb record. In addition to the Red Sox and Mariners, 6 other teams fell on the negative side of the residuals. These teams were expected to have higher runs scored/runs against ratios based on their records. Perhaps they won by close margins and lost by large margins? It’s a possibility!

Despite having a few lucky teams below the zero line for residuals, there were some teams with positive residual values. These teams are the Houston Astros, the Cleveland Indians, the Los Angeles Dodgers, and the Atlanta Braves. Within the context of the data, the positive residuals tell us that these teams had a large runs scored/runs allowed ratio when compared to their win-loss ratio. These teams must have won their games by large margins! That being said, one might consider these teams unlucky; according to the model, these higher runs ratios should have resulted in a better win-loss ratio. In other words, their win totals should have been higher based on their margins of victory. Instead, the proportional amount of wins did not break their way, and their records were not as strong.

In closing, it is important to note that the residual plot has no discernible pattern. Consequently, we could conclude that the linear model is a good fit when comparing Log(W/L) and Log (RS/RA). It was very interesting to see a few deviations from the best fit line, including some of the teams such as the Red Sox, Astros, and Mariners. Hopefully in the near future, I will see my Detroit Tigers among the observations.