It feels so great to be back here on the WordPress blog. After a nice, yet brief, two weeks hiatus from the blog, we have returned to discuss everyone’s favorite genre of statistical figure: the pop chart. Pop charts are popular charts often seen in media, such as pie charts, divided bar charts, and area charts. However, we will see that oftentimes, dot plots provide more pattern and information for analysis than these popular charts.

Our favorite author and statistician William S. Cleveland has stated: “Any data that can be encoded by one of these pop charts can also be decoded by either a dot plot or multiway dot plot that typically provides far more pattern perception and table look-up than the pop-chart encoding.” In this week’s blog post, I will consider two pop charts and use their information to create respective dot plots. As a result, we will notice that the dot plots provide much clearer information for visual analysis.

Part I

First, I will study an interesting and creative derivation in one type of chart: a pie chart made with actual pie! Journalists at NPR conducted a survey in June 2012 about preferences in pie flavor, and compiled the data into a pie chart composed of actual pie slices. The result is seen below:

While this iteration of pie chart is incredibly creative, it might not be as effective in displaying patterns or how close/separated the values are from one another. Consequently, I compiled these percentages from each pie category and created a simple dotplot. The x-axis displays the percentages, while the y-axis partitions each pie flavor. In honor of this past week’s Ohio State-Michigan game, I color coordinated this particular graph in accordance with the game’s victors (I had to, I am an alumnus of Ohio State). As always, graphs look best in scarlet and gray. This recreation is seen below:

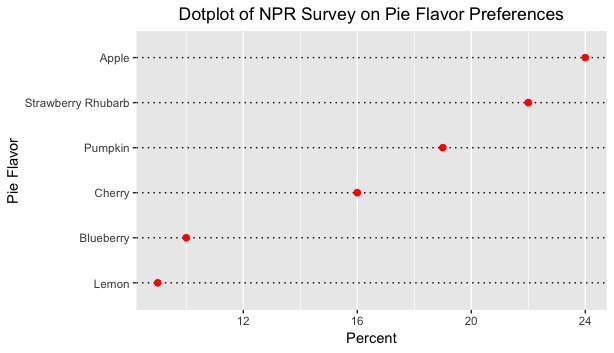
This dotplot provides a much better visual representation of how much separation lies between all of the percentages. A viewer can picture an exact numerical amount of separation between the percentage of apple pie lovers and lemon meringue pie lovers without having to constantly refer to labels or legends. In addition, this dotplot is arranged in ascending order, so the viewer can stratify the categories quickly according to preference. Lastly, the dotplot is very helpful to show how little the separation is between 1) the blueberry and lemon percentages, and 2) the apple and strawberry rhubarb percentages. While one might easily determine this in the original figure, the dotplot provides affirmation to this particular conclusion.

Let’s move onto a topic that is closely related to pie: shark attacks.

Part II

Secondly, I will study an area chart presented by ABC News in 2015. This area chart displays the number of historical shark attacks from the past 430 years, and each circle represents the amount of attacks for each global region. In total, there are 13 global regions presented in the figure. For reference, ABC News includes a scale to compare the circular observations and their areas. This area chart is shown below:

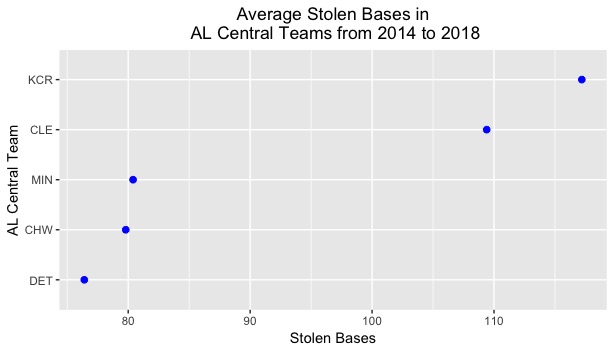
In my opinion, I believe that ABC’s graphics department did a decent job on projecting the area chart and catching the eye of an ordinary newsreader. Including the map in the foreground draw the reader in, while the inclusion of a legend for the area chart allows the reader to compare each observation according to its area. Nonetheless, I posit that a dotplot for the same data would allow for a much clearer comparison among the thirteen regions, and it would permit the viewer the accurately determine the amount of difference of attacks per region.

Using R Studio, I compiled the data of the regions and attacks into a data frame and composed a dotplot of the corresponding information. The x-axis labels the frequency of shark attacks, while the y-axis separates the global regions on their own respective lines. To aid in analysis, I arranged the observation in increasing order. Finally, I color coordinated this figure with maize and blue, to honor the University of Michigan Wolverines. Their efforts this past Saturday were not done in vain. This recreation of the shark attacks data is displayed below:

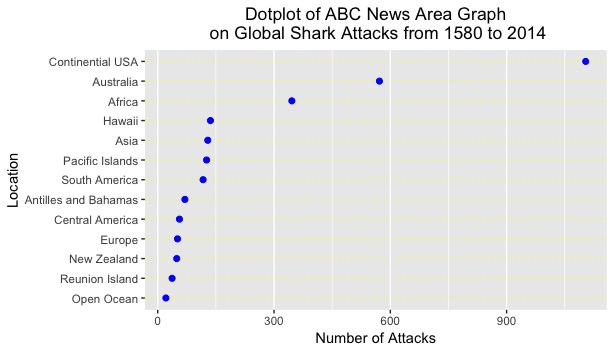
To an average viewer, one might be discouraged in that this figure is not as visually pleasing as the area graph. This figure purely displays raw data. However, the purpose of this figure is to help determine the relationships among the regions and see if any new conclusions can be drawn. One could unequivocally state that this graph does a much better job in presenting the pattern and spread of the observations.

First, one can easily see the magnitude of separation between United States shark attacks compared to the other 12 regions. The USA eclipses all but 2 regions in attacks by more than 1000 attacks, which (one could deduce) is extremely significant. Side note: this phenomenon might be due to 1) more “reported” attacks in the United States and 2) large coastline areas and coastal populations in the continental US.

Second, one can see that there is little spread or variation among most of the regions in shark attack numbers. From the Open Ocean to Hawaii, the range of values hovers from 0 to 150. For a span of 430 years, this range appears to be notably small. In addition, when compared to the Continental USA, Australia, and Africa, these values seem miniature.

Third, this figure is arranged in ascending order, which provides stratification for the regions based on the number of attacks. This was not provided in the area graph and did not allow the viewer to organize the region in a specific manner. I could continue onwards with improvements, but I believe the reasons provided above allot for multitudes of evidence for why dotplots are the superior figures for analysis.

Conclusion

In conclusion, we have seen in the two pop chart figures that dotplot recreations provide a much clearer visual representation of the patterns and spread of the data. While pop charts are pleasing to the eye and allow the viewer to be drawn into the information, they do very little to effectively show any relationships or phenomena between categories or groups. Thus, dotplots are the optimal choice for displaying patterns and relationships for our studies.

This week, I have the pleasure of discussing and analyzing my favorite food: cereal. Before you question my sanity and taste buds, let me first tell you why: cereal is functional, universal, and (on average) delicious. In addition, cereal is an acceptable choice of food for any time for the day. Cereal is the optimal choice of nourishment.

In this assignment, I extracted a table of nutrition facts from US cereals through the MASS library on R Studio. This table included the variables of calories, sugars, carbohydrates, protein fat, sodium, fiber, potassium, and vitamins. For this study, I chose to study the three variables of “calories,” “fat,” and “protein.” I selected these variables because I hypothesize that all 3 variables have positive association among one another. In foods, high calorie foods typically have high amounts of fat. I also conjecture that high fat and high protein foods are positively related to one another (i.e. meats, legumes, nuts, etc.). Using transitivity, I would also assume that caloric levels and protein levels also share a positive relationship, provided there is no conditional independence.

Next, I made three different plots to show the relationship among the three variables. These three plots are a scatterplot matrix, a coplot among different intervals of calorie content, and a 3D scatterplot of the three nutritional variables.

Before diving into these plots, I identified two cereals of interest for this study: All-Brand and Honeycomb. I selected these two because All-Brand contains the highest protein amount per serving, while Honeycomb takes the crown for least amount of protein per serving. Please remind not to eat Honeycomb before going to the gym. These two observations were colored bright yellow in the scatterplot matrix, and colored with bright green on the coplot.

Let’s begin and see if these graphs are grrrrreat.

Scatterplot Matrix

As I hypothesized, it appears that positive relationships exist among each sets of the three variables of calories, protein, and fat. In comparing calories and fat, the trendlines have steep, positive slopes. It is important to note that protein’s positive relationship with calories and fat does not appear to be very strong; the slopes appear to level off toward zero as protein content increases.

As stated earlier, the yellow dots represent those two cereals of interest. Both yellow dots seem to be in the lower range for fat content and calorie content, which is interesting since they have drastically different protein levels. To me, I would have expected All-Bran’s calorie and fat content to be higher since its protein content is large. Maybe All-Bran is a very healthy cereal to consider next time I am at Kroger.

Onto the coplot of our cereals!

Coplot

In this coplot, the condition placed on each viewing window is the calorie content. Each panel represents a different interval of calorie content. In the lower left panel, the cereals with the smallest calorie levels in the sample are clustered, while cereals with the largest calorie levels in the sample are gathered in the top right panel. The cereals increase in calories by interval as one reads from left to right on the bottom, followed by left to right on the top.

Initially, there does not appear to be a noticeably strong relationship between fat and protein in the cereals. There is a steep slope found in the small sample in the bottom left, but it is not significant enough to deduce any relationship among all of the points. In the middle four intervals of calorie content, the slopes are zero or incredibly small; the linear relationship is not very strong among these calorie groups when comparing the variables of fat and protein content.

However, the top right panel provides some significant information. There is a positively sloped trendline in the observations for fat and protein in the highest calorie cereals. One could conclude that, for the high calorie cereals in the sample, as fat content increases, the protein content also increases.

A quick note: the green observations of our capitalized cereals are not easily visible in the coplot. The Honeycomb observation is obscured by data points in the bottom left panel. The All-Bran observation is better seen in the top right panel. While its calorie content is high, its fat content is relatively low for its group.

Finally, we have arrived at the pièce de résistance: the three-dimensional scatterplot.

3D Scatterplots

The next three images are different orientations of the 3D scatterplot. It is difficult to capture the act of rotating the plot, so I was able to take a few screenshots.

Here, one notices that as calories decrease, fat decreases. This matches well with the hypothesis from the introductory statements of this blog post.

In this screenshot, I attempted to attain a diagonal view of the observations. It did not work out too well. However, one can see that as calories increase, the protein content also tends to increase. Again, this orientation is not typical for an average graph viewer.

Here is a third interpretation of the 3D scatterplot. Once more, as calorie content increases, protein content tends to increase.

Conclusion

I was very thankful for this opportunity to study these three nutritional variables for the sample of United States cereals. I was able to see that my hypothesis was true: there is a positive association all among calorie, protein, and fat content. To me, I found the scatterplot matrix to be most useful for analysis. The viewing windows were very clear and the labeling and structure seemed very intuitive for me. I also enjoyed working with the three-dimensional scatterplot and rotating the figure to see how all three variables are associated as a single unit. The difficulty in this plot was providing aesthetically pleasing two-dimensional screenshot images for the post.

One last thing: All-Bran seems to be a healthy cereal! Despite its high calorie content, it is high in protein and relatively low in fat. It seems like I’ll have a new breakfast of choice.

For the first time this semester, I had to scramble to make sure that my blog assignment was complete for this week. At the school where I teach, both Halloween and parent-teacher conferences presented themselves as new schedule challenges for me. As a result, I had to complete my blog in the afternoon hours of Friday. I never procrastinate, so obviously this is an unusual set of circumstances. Let’s see if I can pass this latest challenge.

This week in Cleveland’s text, we read over content on time-series plots and the use of color in differentiating graphs. Relatedly, our blog assignment this week pertains to using color while graphing plots in R. Thanks to some advice from Dr. Albert, I was able to make sure the graphs I present are accurate. This week’s blog is broken into two parts: Part A describes a time-series plot comparing Broadway attendance numbers, while Part B discusses a contour graph of the density of a bivariate normal distribution.

Part A

In the first part of this week’s entry, I looked at data from Broadway shows of the past twenty six years. I was very interested to see the relationship between the three main genres of shows: musicals, plays, and specials. Particularly, I was curious to see how their average attendance numbers compared for each year. Initially, I expected musicals to have by far the largest average attendance numbers. This is due to their popularity and relevance in the American zeitgeist compared to plays and specials.

To create the plot, I first calculated the average attendance numbers by year for each of the three genres. This was found using an aggregate function in R. Then, I create a time-series plot of the average attendance numbers by year, grouping by genre. The red line represents the time-series of musical attendance, the blue line represents the time-series of specials attendance, and the green line represents the time-series of play attendance. The figure is seen below.

Not surprisingly, musicals have had large average attendance numbers the past twenty six years. However, there appeared to be a drop-off in average attendance during the mid 1990s. This could be due to the increasing popularity in television and video games as other forms of media. Plays have had a relatively stable attendance series. There was a brief spike in play popularity during the early 1990s, but then the average attendance numbers level out around 5000 for the remaining twenty years.

The “specials” genre has been the most surprising of the three. Specials had a dramatic decrease in average attendance during the early to mid 2000s. However, their popularity spikes up extraordinarily from the mid 2000s to present day. This could be due to increasing popularity in specials such as celebrities performing one-man shows, anniversary specials of Broadway shows, stand-up comedy routines, etc. These types of intimate and unique performances tend to garner steam and attention through social media and YouTube, and thus could result in higher attendance numbers.

The differentiation in color for the three groups made the graph very easy to interpret. There were no unusually close colors or values that would cause for any misreadings. As a result, selective color choice is a smart decision to make when plotting multiple time-series on the same figure.

Onto our next section!

Part B

In Part B, I entered the simulation code for a bivariate normal distribution into R, which was given to me by Dr. Albert on the Canvas website. In his initial code, Dr. Albert selected a color palette which represented a traditional rainbow spectrum. While the figure looked very pleasing to the eye, it did not seem to be most effective for representing the density in the normal distribution.

In my figure, I decided to color the density plot with different shades of purple. As the density level increases, the purple color of the plot becomes lighter. The figure is shown below.

I find this plot to be very effective in showing the different levels of density. First, the change in density appears more fluid/continuous in the purple plot than the rainbow spectral plot. This is due to the similarity in purple colors. Second, I find that choosing similar colors allows the figure to be less distracting. Multiple varying colors can muddle the plot or confuse the viewer into thinking there is a sharp/dramatic change in density. The contrast between colors such as red and blue in the original plot allow for easy differentiation, but the average viewer might misconstrue these different color changes as vast changes in density.

In this assignment, I was able to better understand that color choice is very important when creating figures. Ultimately, it depends on the context of the graph. Similar choices in color are useful when comparing similar units with slight changes, while different colors are useful to analyze time-series or plots of differing categories. In addition, I was also able to learn personally that it is not optimal to wait until Friday to complete a blog assignment.

This week has provided a golden opportunity for me. Unlike past assignments involving familiar graphs and topics such as baseball and Broadway shows, this week’s assignment allows me to explore some unfamiliar territory. Truth be told, I have never used R to perform a loess smooth on a scatter plot. This week changed everything.

Let’s get started.

Loess Smooth on a Scatterplot

To achieve our x and y values for the initial scatterplot, I read a function into R Studio from the Canvas module. This function simulates some (x, y) data where the true signal follows one of the curves sin(x) + cos(x), sin(x) – cos(x), sin(x) * cos(x).

After reading in the simulated data, I plotted the points onto a scatterplot using ggplot under the Tidyverse R library. Subsequently, I overlaid a Loess smooth curve on the observations. For this figure, I used the default setting for span. This first figure is seen below:

I am a big fan of the Loess smooth over this data. The observations follow a curve trend (understandably, since the read-in function is trigonometric), and a Loess curve perfectly captures this general trend.

To see if this curve is an acceptable fit, I plotted the residuals for this scatterplot. My hope was to see randomness exists in the residual plot. In addition, I included the trend line for the residuals. If the residuals are truly random, then the trend line should lie completely horizontal along the line y = 0.

Residual Plot

The residual plot is shown in the figure below. In this figure, the line y = 0 is green while the trend line is in blue.

The residuals, at first glance, look to have no discernible pattern. This is a good thing! That must mean that the Loess smooth is a good fit for the data. However, the trend line is not perfectly horizontal; the slope is slightly positive. Thus, I deduced that there could be a possible Loess curve which more accurately represents the path of the x and y observations. The residuals provide strong evidence that the current Loess smooth is acceptable; however, it can be improved.

Loess Smooth (Span – 0.15)

In this next Loess smooth, I adjusted the span value of the function from its default setting to a value of 0.15. As a result, with a decreased span value, I anticipated the new curve to be less smooth. The result is seen below:

My premonition was correct in that the curve with the new span value is less smooth than the default curve. More prominent ridges are seen in this figure. However, I believe this figure is a better fit for the data since these ridges allow for the best-fitting line to become closer to the observations. To confirm this belief, I plotted a second residual chart, considering the new span value of 0.15.

While it does not initially appear that the residuals are more or less random, the trendline allows the viewer to differentiate their values from the initial residuals. This trendline appears to be perfectly overlaid on the line y = 0; in other words, the trend line for the residuals is now completely horizontal. This means that the residuals are more random that the residuals from the previous curve. The adjusted span of 0.15 in the new Loess curve allows for more variability in the residuals; thus, the adjusted Loess smooth is a much better fit for the trigonometric data.

In this assignment, I discovered that changing the value of the span in the Loess function allows the function to become more or less smooth. As a result, the change in span also adjust the values of the residuals. In this particular study, the change in span allowed for a better fitting curve and more randomness in the residual plot.

For those who do not know, I am a life-long baseball fan. I have been to over 200 Detroit Tigers games since my infancy. I can tell you Miguel Cabrera’s career batting average and Justin Verlander’s 2011 season statistics. I might as well have the lyrics to “Take Me Out to the Ballgame” tattooed on my forehead. As a result, you might guess that I would choose to conduct my analysis on Major League Baseball, especially in the midst of this year’s ALCS and NLCS games. Particularly, I have chosen to study the five teams from this world’s finest sports division: the American League Central.

The AL Central is comprised of some of baseball’s finest franchises: the Chicago White Sox (CHW), the Cleveland Indians (CLE), the Detroit Tigers (DET), the Kansas City Royals (KCR), and the Minnesota Twins (MIN). In this study, I decided to focus strictly on the number of stolen bases during the past five seasons for these five teams. Using Baseball-Reference.com, I compiled the stolen base numbers from each team for the 2014 through 2018 seasons. Consequently, the data was organized into a 5×5 two-way table, with teams representing the rows and the seasons representing the columns.

One might posit the question: “Why choose stolen bases as the statistic of study? Why not popular choices like wins or runs or batting average?” First, stolen bases have a positive correlation with runs scored, and consequently, wins. This is because that stolen bases provide information that either a runner advanced to scoring position, or the runner scored from third base. Second, the AL Central has an interesting collection of teams in regards to their public perception of baserunning. Kansas City and Cleveland are known for their strong base running, while the Detroit Tigers are well-known for their baserunning foibles (particularly in the playoffs). Thus, I wanted to know if these stereotypes are accurate for these teams.

As always, the charts were made using R Studio and the tidyverse/ggplot libraries.

Chart #1

First, using the 5×5 table, I calculated the average stolen bases numbers from the past five seasons for each team. Then, I made a simple and straightforward dot chart (Cleveland-style, of course) with the five averages. It is seen below:

As one can see, the means are arranged from lowest to highest. This allows a comparison among the five teams to be easily made. As I initially predicted in the introduction, Kansas City and Cleveland are extreme leaders in average stolen bases during this period for the division. KC has approximately 117 stolen bases per year, while Cleveland has about 109 stolen bases per season. On the other end of the spectrum, the three remaining teams all hover in the 75 to 80 range for their averages. Notably, my personal favorite Tigers average about 77 stolen bases per season from 2014 to 2018. This does not come as a surprise; after watching the frustrating Bless You Boys for years, I am well aware of their baserunning issues.

Next, we will consider each season’s observations, grouping by team.

Chart #2

In this chart, each stolen base observation is listed. Thus, there are 25 total observations on this plot. Each y-value corresponds to the AL Central franchise, while the x-axis values correspond to the single season’s stolen base numbers. To help differentiate between the observations, the seasons are color coordinated and the point shapes are open circles. The open circles help provide visual clarity, should there be any overlap and proximate values.

This beautiful plot is shown below (full disclosure: Dr. Albert’s assistance in this particular plot was a significant help. I am extremely grateful).

There are a lot of conclusions that can be made from this plot. First, I find it very noteworthy that Minnesota only stole 47 in the 2018 season. Typically, their stolen base values per season hovered around the 90 to 100 range for this period. This most likely pulled the average stolen base value down for them, as seen in Chart 1.

Second, the ranges for each team are much larger than I anticipated, with the exception of the Chicago White Sox. The ranges for the four other teams have sizes of 40 or 50 stolen bases. There is a lot of variability with these numbers, which could be attributed to changes in coaching, head-to-head matchups, roster changes, etc. Stolen base numbers can be greatly affected by these factors in major league baseball.

Third, I noticed that the maximum value of any season is the Kansas City Royals’ 2014 season of 153 stolen bases. This is incredibly large. Since the baseball season is 162 games, one could reasonably assume that Kansas City stole close to one base per game, which is unusually high. Interestingly enough, the Royals won the American League this same year. Perhaps this large stolen base number had an effect on their runs scored/win total? It’s definitely something to consider.

Fourth, I noticed there is a slight overlap in observation for the 2016 and 2018 Cleveland Indians in their stolen base values (134 and 135 stolen bases, respectively). Since I made the shapes open circles for the figure, one can easily distinguish between the two observations. Relatedly, the Cleveland Indians won the AL Central in both of those seasons. As with Kansas City in 2014, these high stolen base values might have an effect on team success.

Chart #3

For this third figure, I grouped the data by season, with each season from 2014 to 2018 on the y-axis. Similarly to the previous two figures, the x-axis represents the stolen base values for each season. Each individual data rectangle displays the five stolen base observations for each American League Central team.

First, I find it interesting that there is no overarching trend for stolen base numbers as the seasons move up from 2014 to 2018. One could possibly deduce that there is no specific correlation with the season and stolen base numbers (at least for the American League Central). I do find it interesting that the Tigers’ stolen base totals decreased from 2014 to 2016, and then slightly increased in 2017 and 2018. Perhaps this is a sign of improvement for the recently beleaguered Detroit squad? One can hope!

Second, it appears that Cleveland has some “overcorrecting” habits for their stolen base totals. In 2015 and 2017, their stolen base numbers were 86 and 88, respectively. Humorously enough, their stolen base numbers in the following seasons of 2016 and 2018 were 134 and 135, respectively. It seems that Terry Francona must have preached base running during those off seasons .

Third, I find it interesting that at least once in the past five years, each AL Central team has had a season of around 100 stolen bases. This is true for both the good and bad baserunning franchises. Does this provide us any new information? Possibly. Perhaps 100 stolen bases serves as a good measure of center, or a value of high density for AL Central teams during the past five seasons. This can be determined in a future exercise, of course.

Conclusion

In this study, each of these figures provided useful pockets of information. Chart #1 is helpful due to its simplicity and allows for a quick summary of data. Tyro statisticians and inexperienced readers would enjoy this graph because its small data size and ascending order allow for simple and quick analysis.

Chart #2 is useful because it shows the variability and ranges of the data per team. Grouping by team allows the reader to visually compare the stolen base numbers among each American League Central team. In addition, no specific observations were omitted from the figure, as were the case in Chart #1.

Chart #3 is beneficial because it permits the reader to determine any trends through the 2014 to 2018 seasons for each team (as mentioned earlier, there is no discernible trend). The vertical scale lines passing through each scale rectangle also allows the reader to compare similar or vastly different observations among AL Central teams in the same column.

To me, I found Chart #2 to be the most beneficial for analysis. Grouping by teams allows for better analysis because one can see the center, shape, and spread of the observations for each of the five teams. In addition, since the plots are on the same scale rectangle, their distributions can be easily compared to one another visually. Chart #3 is useful, but the partitioning by team into five viewing windows makes analysis more challenging. Thus, when comparing American League Central teams, grouping by team seems to be the more optimal route for analysis.

In conclusion, I found the data from the past five seasons to be fascinating. In addition, some of my preconceived notions about the AL Central teams were confirmed. Kansas City and Cleveland have strong stolen base numbers from year to year, while Chicago and Detroit have room for improvement in their baserunning (Minnesota’s distribution stayed mostly centered, with the exception of th 2018’s outlier). In future exercises, I would love the see the total distribution of the division’s baserunning totals.

I am sick today. I’m not editorializing or being dramatic: I had to call into work today due to unexpected head cold. The benefit of my faulty immune system? I had the opportunity to work on this week’s blog post. Working full-time while taking some grad classes is a fun challenge, but I do relish the chance for some extra time to work while I recover.

Enough about me, though. This week, we are studying sampled data from students in an introductory statistics class. Since my first name starts with the letter “N,” I was charged to study the relationship between gender and the number of shoe pairs owned by each student. First, I took a random sample of size 100 from the group, using software from R Studio (full disclosure: R Studio was used to code and create the figures in this assignment). Next, I filtered the data by gender and shoe size into two data frames: one frame for men and their shoes, and a second frame for the women and their shoes. With my new vectors in place, I was all ready to create some figures using R Studio. Let’s dive in!

Parallel Dot Plot

First, I composed a parallel dot plot for the shoe pairs, organized by gender. Dot plots are nice because they are very difficult to misinterpret. They are one-dimensional and can quickly show the values and spread of the observations. Dot plots are the vanilla ice cream of plots: a true classic for numerical data.

However, as one can see below, this dot plot has some visual issues.

The obvious issue is that many of the observations obscure or completely overlap each other. As a result, we cannot accurately visualize how many observations exist in the sample nor what their exact values could be. Nonetheless, I can still make some conclusions from the plot. The male observations seem to have little variability and are clustered in the 1 to 20 range. The female observations have much greater variability, extending from about 5 to 100. These female observations, similarly to the men, do have congestion in the 1 to 20 range.

While the plot gave us some pockets of information, it was far from perfect. Onto the next figure!

Parallel Quantile Plot

The second plot on our journey is a set of quantile plots included in the same scale line rectangle. Quantile plots help add an extra dimension to our data. On the x-axis, I have broken the labels into fractions from 0 to 1. On the y-axis, the quantiles (i.e. equal sized groups for the distribution) are labeled. To make sure the data is organized in an increasing fashion, the observations for the male and female data frames are arranged in ascending order. In essence, we are just plotting the quantiles of the two distributions.

This figure provides more clarity than the previous dot plot. First, a legend is included to differentiate the two types of points. Second, no data points are being obscured and we can clearly see the shape/trend of each group. While both groups move upwards as the fraction values approach one, the female values on average are much higher than the male values. The female observations are greater than the male ones ranging from 5 to 15 quantiles, which is a considerably large range since this figure is broken into 20 quantiles in total. It is also important to note that many female and male observations fall within the same quantile. A group of six men fall under the third quantile and a group of eight men fall on the fourth quantile, while nine women lie on the 15th quantile and eleven women fall along the 20th quantile.

What could be deduced by this graph? In this introductory statistics class, female students on average have many more shoes than the male students.

Quantile-Quantile Plot

While the second plot provided plenty of additional information to me, I was curious to see if other figures could provide any new insights. A quantile-quantile plot is a nice brand of scatter plot which compares the quantiles of male shoe pairs on the x-axis and the quantiles of female shoe pairs on the y-axis. For this plot, these quantiles are broken down by a group of size 15 so that the two categories can be properly compared despite their different sizes. Subsequently, one can see that there are only fifteen observations in the plot below.

Luckily for this plot, the observations only have one obstruction; in addition, this obstruction does not deny us the possibility of determining the two values. On this figure, the line y = x is included as a reference. If the points fell along this line, we could deduce that male and female shoe amounts have virtually no difference. One can see that this is not the case. Every single observation lies above this reference line, which means that on average, female shoe amounts are much higher when compared in ratio to the male shoe amounts. After conducting some visual analysis, that there is no constant difference between female and male shoe pair amounts. These differences between x and y increase as the observations move to the right. In other words, female students with a small amount of shoes have little difference than male students with a small amount of shoes. However, if a female student and a male student each has a large amount of shoes (relative to their categories), then the difference between their amounts is massive.

Tukey Mean-Difference Plot

To confirm this notion that the female-male difference in shoe pair amount increases as the number of pairs increase, I created a Tukey mean-difference plot. On the x-axis, the mean of the female + male shoe pairs are plotted, while their difference is plotted on the y-axis. The fourth figure in our study is seen below:

Based on this increasing trend, my initial analysis appears to be corrected. As the number of shoe pairs increase for each male and female, then the difference between their values also increase. That being said, these differences between female and male shoe amounts tend to all fall under a specific value. With the exception of two observations, these differences fall below 20 (as shown with a purple horizontal line in the figure, for reference). In other words, most female student have less than 20 more shoes than their male counterparts. With the observation on the far right, the female student being studied had 35 more shoes than the male student with the largest amount. Wow!

What relationship can be determined here? For one, female students tend to have more pairs of shoes than their fellow male students. Second, the differences in shoe pairs increase at their means increase. In other words: there is a big gap between the larger values for females and males, respectively. This could be a result from the large variability in female data and small variability in male data.

Conclusion

All four graphs provide a glimpse into the relationship between shoe pairs in male and female students. The dot plot gave us a nice glimpse into the raw data distribution; however, many of the data points obscured each other. I would argue that this figure, among the four included in this post, was not the best for analysis.

The parallel quantile plot was very helpful to determine how the observations trend for each category and helped us determine that female observations were noticeably higher than the male observations for shoes. However, this graph could not tell us the sizes of their differences. As a result, the qq-plot and the mean-difference plots were able to extend from that data and explain the change in differences.

Myself, I would argue that the mean-difference plot was the most helpful for analysis. This plot showed the exact values of male-female differences, and it confirmed my initial conclusion that the differences increase as shoe pair amounts increase. It also gave me a glimpse into how close some of these differences were (i.e. a majority of the differences fell under 20). While one could argue that a qq-plot could provide the same information (which is true, to be honest), I personally found the mean-difference plot easier to analyze.

In conclusion, the sample and the four graphs provided a nice window into shoe pair amounts for male and female students in this introductory statistics course. From this study, we saw that on average, female students own more pairs of shoes than male student. In addition, as the number of pairs of shoes increased for each gender, the difference between their amount also increased. This is mostly attributed to the large range and variability found in the female students’ observation in shoe amounts.

A crisp chill enters the air. A bowl of nachos appears atop my couch-side table. The soothing sounds of John Stirling creep into my ears. Why yes, it is October 2nd: the official start of the 2018 Major League Baseball postseason.

I have been a lifelong fan of baseball, and relatedly, a lifelong fan of baseball statistics. I am all too familiar with Bill James and his revolutionary handbook, paving the way for sabermetric-focused scouting, team-building, and analysis. One of these revolutionary formulas include the Pythagorean relationship, which explains the connection between the logarithmic ratios of both 1) wins to losses, and 2) runs scored to runs against. I couldn’t wait to begin this assignment, despite my favored Detroit Tigers not being studied.

For reference, here are two variations of the Pythagorean relationship:

And, in logarithmic form:

As one might guess, we will need to determine this value of k!

I decided to study 12 Major League Baseball teams from the 2018 season. These twelve teams were not randomly sampled; I selected the teams with the 12 best records in the majors. These twelve teams, in addition to their wins, losses, runs scored, runs against, etc., are shown in the image below. Specifically, I extracted these values from ESPN.com:

I was mostly intrigued by this year’s data because there were some noteworthy accomplishments among the top teams. First, the Boston Red Sox won an unusually large 108 games in the regular season. I was very curious to see if their ratio of runs would have been the major contributor for their success. Second, the 12th best record belongs to the Seattle Mariners, who surprisingly have a negative run differential. This seems very unusual for a team with 89 wins, and I wanted to see how extreme their residual value would be. Third, there were many teams (6 to be exact) who all had wins in the 89 to 92 range. I am excited to see how their Runs Scored/Run Allowed ratios and their residuals compare to one another.

Not that it is very important, but I included a screenshot of the Excel Workbook I used for these twelve teams. I now included some additional columns for the teams, which are Win/Loss ratio, Runs Scored/Runs Allowed ratio, and the logarithms of those values. This screenshot is shown below:

Let’s get to work!

I saved the Excel work as a CSV and read the file into R Studio. Then, I saved the information into two data frames: the first dataframe held the values for Log(W/L) and Log(RS/RA), while the second data frame held values for the residuals when compared to Log(W/L). In creating these dataframes, I had some guidance thanks to Dr. Albert (thanks again!).

First, to help determine the best value of k, I created a scatterplot comparing Log(W/L) and Log(RS/RA). It is shown below:

Before I calculated the value of k (which in this case is the slope, since k is the value of the exponent when a logarithm is not applied), I noticed that there were some observations which deviate from the best fit line. Thus I predicted that some big residuals will occur!

My calculation of k will not be perfect, but it will be relatively accurate. Two coordinates along the line I chose were (0.10, 0.05) and (0.15, 0.076). Using the formula for slope, k is calculated to be 0.52. In other words, for every unit increase in Log(W/L), the Log(RS/RA) ratio also increases by a value of 0.52.

Next, I created a Figure with R Studio similar to that of Figure 3.5 in the textbook. The top figure is the one which I discussed above. The bottom figure is a residual plot for the two ratios. This fancy little figure is shown below:

As predicted earlier, there are some big residuals here! The negative residual on the far left represents the infamous 89-win Mariners. Their residual lies so far below the residual line due to the fact that their run differential is a negative value. This affected their Log(RS/RA) ratio, as seen in the scatterplot in the top figure; their observation falls below 0 and well below the best fit line. This team is very lucky though. Despite a negative run differential and log (RS/RA) ratio, they ended up with 89 wins! That is very impressive.

One other unusual residual is the negative residual at approximately x = 0.30. Wildly, these observation belongs to our talented Red Sox team! This residual tells us that while their Win Loss ratio is large, it does not result in a proportionally large run differential or ratio. In other words, the Red Sox were expected to have a better runs ratio based on their superb record. In addition to the Red Sox and Mariners, 6 other teams fell on the negative side of the residuals. These teams were expected to have higher runs scored/runs against ratios based on their records. Perhaps they won by close margins and lost by large margins? It’s a possibility!

Despite having a few lucky teams below the zero line for residuals, there were some teams with positive residual values. These teams are the Houston Astros, the Cleveland Indians, the Los Angeles Dodgers, and the Atlanta Braves. Within the context of the data, the positive residuals tell us that these teams had a large runs scored/runs allowed ratio when compared to their win-loss ratio. These teams must have won their games by large margins! That being said, one might consider these teams unlucky; according to the model, these higher runs ratios should have resulted in a better win-loss ratio. In other words, their win totals should have been higher based on their margins of victory. Instead, the proportional amount of wins did not break their way, and their records were not as strong.

In closing, it is important to note that the residual plot has no discernible pattern. Consequently, we could conclude that the linear model is a good fit when comparing Log(W/L) and Log (RS/RA). It was very interesting to see a few deviations from the best fit line, including some of the teams such as the Red Sox, Astros, and Mariners. Hopefully in the near future, I will see my Detroit Tigers among the observations.

I long wondered when my days of dancing and singing in the high school musical would come into handy. Luckily, this week’s assignment examines the data for Broadway musicals. While my old dance shoes won’t come in handy here, my prior statistical skills and thirst for improved theatre knowledge should play as a featured role.

I downloaded the CSV file from the given link and began to analyze the data, particularly from both periods of 2000 to 2008, and 2009 to 2016. In this study, we are asked “what makes a Broadway show the best?” While it is almost impossible to qualify a work of art as “best” (that’s an argument for another class), we can use some parameters that would give us a glimpse into their popularity and feature in the zeitgeist.

I had considered attendance, number of weeks performing, size of the theatre, and several other factors for the “best” descriptor. However, I decided that “gross income” for the show would be an excellent indicator. Current blockbusters like Hamilton and The Book of Mormon not only have high attendance numbers, but they also require the theatregoer to dole out large amounts of money per ticket, due to high demand. Gross is positively correlated to attendance, as one might imagine, but I would also wager that gross and ticket price (and tangentially, demand) share some positive correlation.

To compare every single Broadway show by gross income would indeed be a gargantuan task; as a result, I am only comparing highly grossing shows. In my study, the shows displayed in the figures have cumulatively made over 200,000,000 dollars. This reduces the number of shows, which makes it easier to analyze.

I used RStudio to make my graphs. First, I have a set of grouped bar graphs included below. The first graph is a bad one. Let’s take a look at it:

Do not adjust your computer screen; I am well aware that there are some issues with the graph. First, the labels are all clustered together on the x-axis. It is impossible to read which shows are being presented. This can be fixed by changing the location of the x and y-axes. Second, the x and y labels need to be interchanged. Third, the title is acceptable, but it might be useful to declare that this is a grouped bar chart. Upon looking at these mistakes, I made some edits and the new final product is seen below:

This graph is much improved compared to the first one presented. First, the x and y-axes have been switched, allowing us to read the bar labels without any obstruction. Second, the axis labels are in the correct location. Upon looking at this graph, The Lion King is the highest grossing Broadway show in both the 2000-2008 and 2009-2016 periods. The show Wicked comes second in total gross among the periods, with The Book of Mormon rounding out as the third highest grossing show. To a Broadway fan like myself, this makes sense: The Lion King and Wicked are often considered in the theatre wing to be the most popular shows of the past two decades, and these Tony-Award winning shows are highly acclaimed by audiences and critics.

I was curious to see the stacked bar charts for this data, since several of these shows have runs spanning throughout both periods. As a result, I created two versions of this specific type of chart: a “bad” version and a “good” version. The bad version is displayed below:

You can deduce why this would be considered the “bad” version of the graph. First, the graph does not have a title. To the common viewer, one might not know what the graph is display, aside from gross. The y-axis label “Name” also does not provide enough context to the average viewer. Second, the stacked bars are not arranged in size order, which makes it a little more difficult (while not impossible) to analyze. A positive of the graph? A legend is provided outside the data rectangle, and the axes are correctly labeled. The second graph, seen below, improves on those identified mistakes:

As one can see, the title of the graph provides context of 1. the type of graph, and 2. the exact data being studied without any confusion. The data has been arranged in decreasing order, with the largest total gross on the top of the graph and the smallest total gross income on the bottom. The graph arranges the data according to largest total gross per period as well. This characteristic can be seen when comparing The Book of Mormon and The Phantom of the Opera. The Book of Mormon is placed higher on the graph due to the fact that it had a higher gross within a single period; that being said, The Phantom of the Opera had a higher overall gross throughout its entire run.

As stated with the grouped bar charts, The Lion King has the record for largest overall gross within the two periods. By my own criteria, The Lion King would be considered the best Broadway show from 2000-2008 and 2009-2016. The show has amassed almost 1.25 billion dollars in ticket sales during its run. There are some other shows with high gross incomes that could claim the title as “best.” Wicked, like the Lion King, has grossed over 1 billion dollars and has immense global popularity. The Book of Mormon, while only active in the 2009-2016 period, has grossed just under 500 million dollars, which is one of the largest values for a single period. Based on my own parameters, the “best” shows in these periods would be The Lion King, Wicked, and The Book of Mormon.

Upon learning that this week’s assignment was pertaining to population growth, I was ecstatic. Population studies have always been an interest of mine, but I have mostly focused solely on city and state populations of the United States. This assignment provides a nice blend, mixing my interest in populations with my unfamiliarity of world growth patterns.

Part I.

In my first part of analysis, I gathered data and a CSV file of countries’ population data over the past 57 years. To simplify the calculation and figure construction, I only selected a 10 year period for analysis. I chose the interval 1997 to 2006. To be honest, there is no specific reason why I chose this ten year period; it is purely arbitrary. Perhaps the selection of 2006 is a unconscious attempt to remind myself that my favorite sports team, the Detroit Tigers, lost the World Series in 5 games in that year. Who’s to say?

For analysis, I chose to study the country of the United Arab Emirates. Primarily, this is because the United Arab Emirates, or UAE for short, is noteworthy for its rapid population growth. This growth is most famously seen in its city of Dubai, where its population gained 600,000 people from the span of 1995 to 2005. I conjectured that population growth in the UAE from 1997 to 2006 would be exponential, and thus determined the country to be the most interesting for this study.

Using R Studio, I graphed the yearly population data from 1997 to 2006 using line graph. On the horizontal axis, each year was plotted. For the vertical axis, two different scales were used. On the left vertical scale, the logarithm (base 2) of the population is represented to best analyze the growth rate. On the right vertical scale, the population itself is represented. The figure I created is seen below:

There are several noteworthy observations made from this graph. First, the graph looks linear with a constant slope from the years 1997 to 2002. Using the points at 2002 and 1997, I was able to make a quick visual calculation of the slope, which is approximately 0.08. This means that the growth rate each year from this span, converting from logarithm base 2, would be 2^0.08, or 1.057. In other words, the average growth rate would be 5.7% per year. As someone who lives in the Rust Belt in 2018, this rate is massive!

However, this slope does not even represent the largest period of growth! The slope no longer becomes linear and follows an exponential pick-up from 2003 to 2006. At its steepest, from 2005 to 2006, the slope of the line is approximately 0.2, which corresponds to a growth factor of 1.149. That is a massive 14.9 percent in one year!

Lastly for this graph, it is important to know that these population sizes are not miniscule: they start at 2.75 million to nearly 5.25 million by 2006. Gaining 2.5 million people in decade, for a small country area-wise, can have major repercussions for the UAE’s infrastructure and public policy. Population growth can be very beneficial for a nation, particularly for their economy, but extremely rapid growth can sometimes be met with disastrous economic bubbles and crashes.

Part II.

For part II, I decided to compare the population of the UAE with another country. The second country I chose was Honduras. The reasoning was twofold: first, Honduras has a similar reported 2017 population size to the United Arab Emirates. Second, I wanted to compare the population trends of a West-Asian country with a Latin American country, since both areas have seen positive trends of population growth in the past few decades.

Once more using R Studio, I plotted the two countries’ populations from 1997 to 2006. On the horizontal axis, the year is represented, while the logarithm base 2 of the population is represented on the vertical axis. Only one vertical scale is used for this graph, as shown below:

The shape of the UAE graph should have no surprising characteristics, considering we studied this trend in part I. However, it is intriguing to compare the UAE trend to the Honduras population trend. Throughout each year from 1997 to 2006, the slope of the UAE graph is greater than the slope of each year for the Honduras graph. Thus, we can conclude that the UAE’s population growth rate is greater than Honduras’s rate, even though the population is smaller. Should these rates continue, it would be reasonable to assume that the United Arab Emirates will pass Honduras in total population. (Author’s note: this leapfrog in population happened in 2010)

Secondly, it is noteworthy that Honduras’s population growth is perfectly linear from 1997 to 2006; thus, each year’s rate should be approximately the same. Performing a quick calculation for Honduras, with the years 1997 to 1999, the slope was found to be 0.025, which corresponds to a growth factor of 2^0.025, or 1.017. This translates to a 1.7% growth rate, which indeed much smaller than any of the UAE growth rates determined in part I.

Is it possible to make a general conclusion about West-Asian and Latin American population trends based on this single graph? Absolutely not. Only two sets of population data for a small span of years does not provide enough information to speak for entire global region’s growth. However, it does provide a specific glimpse into these two countries and their particular growth rates. These rates can also help one create predictions for their future populations.

Part I.

In this blog, I will be creating two graphs comparing the caloric and sugar content of United States cereals. First, I created a scatterplot using the ggplot2 feature in R Studio. I was able to clearly plot the observation and provide the graph with detailed labels and a title. The final product is shown in the image below:

The purple data observations show a steep, increasing trend. In general, as the amount of calories per serving increases for the cereal, then the number of grams of sugar is likely to increase. There are two particular outliers found on the far right of the graph; that being said, those specific high calorie cereals also result in a higher sugar content. From this data and its overall trend, we can deduce that high calorie and high sugar content in cereals are strongly, positively correlated.

Next, I created a second scatterplot using the identical data set. However, for this particular plot, I made some slight adjustments which violate the principles of “Clear Vision” found in the Cleveland textbook. This adjusted graph is shown in the figure below:

Within this graph, one can see that there are several violations to the “Clear Vision” principles. First, it violates the principle of “use visually prominent graphical elements to show the data.” These observations are much too small to be noticed by the naked eye. Additionally, the colors of the observations are too bright, which makes it more difficult to be discerned.

Second, the graph violates the principle of “do not clutter the interior of the scale-line rectangle.” For this graph, I added two labels: “cluster of observations” and “observations lying outside the cluster of data.” These labels not only are unnecessary, but they provide too much information for the scale-line rectangle.

Thirdly, the graph violates the principle of “do not allows data labels in the interior of the scale rectangle to interfere with the quantitative data.” These labels, while possibly useful for an average viewer, obscure the data points and can cover up important data values or outliers. This can affect a viewer’s interpretation of the figure and provide contradictory analysis. As one might gather, these additions to the new graph create more drawbacks than benefits for data analysis.

Part II:

In Part II of this post, I have decided to include a third variable in the analysis: number of fat grams per cereal serving. I figured that fat content would be related to both calorie and sugar content in cereals. In this figure, the purple squares represent the sugar observations when compared to calories per serving, while the red triangles represent the fats observations when compared to calories per serving. The analysis comparing the two variables of sugar and fat is shown in the figure below:

In this figure, we can easily differentiate between the two types of observations. The shape, sizes, and colors allow each observation to be distinguishable from one another. Thus, we are allowed to make some conclusions from the data. In this graph, we can see that the trend for caloric and sugar content is much steeper than the trend for that of caloric and fat content. In terms of grams, there is much more sugar found in cereals than fats, per serving size. Using this information, one could conclude that sugar plays a larger factor in cereal consumption than fat.

This does not mean that the graph is perfect. First, I was unable to create a legend from R Studio. Without my preface, the viewer would be unable to discern between the two types of observations and could possibly lead to a different conclusion. Second, there are some fat serving observations which overlap and obscure individual data points for sugars. While this would not affect the shape of the overall trend, this might cause an adjustment should one perform measures of central tendency or variation.

Nevertheless, the graph performs an effective comparison between the two variables of sugar and fat content, when both being compared to caloric content. The viewer is able to make conclusions from the figure, namely that sugar content is much higher per calorie than fat content per calorie.

This week, I was able to construct a scatterplot with academic term on the horizontal axis, and the logarithm of the instructional fees on the vertical axis. The raw data is seen below:

YEAR  FEES
1960  $100
1971  $170
1980  $306
1990  $1146
2000  $2157
2010  $4161
2018  $4548

Using R Studio, I created a data frame and used the tidyverse library features to create a plot with the table. To mix things up, I changed some of the features of the plot. I made each observation an orange color with a square shape. For the segmented lines connecting the observations, I increased the line thickness so that it may appear more visible. The horizontal and vertical axes were labeled as “Academic Year” and “Log of Instructional Fees, in US Dollars,” respectively. The title of the plot was re-named to “A Scatterplot of Bowling Green State University Instructional Fees Per Academic Year from 1960 to 2018.”

The final product is seen below:

From this plot, we can determine that instructional fees have consistently increased from the year 1960 to 2018. Particularly, I notice a sharp increase between the years 1971 and 1980, and an additional large jump between 1980 and 1990. This most likely reflects the value of the US dollar per year and the rising expenses of higher education. It is wise to note that from 1990 to 2010, the rate of increase for instructional fees appears to be mostly constant. However, since we are working with only three total observations in this interval, we cannot definitively conclude that this is the case for every year. One last important trend I noticed is that the rate of increase is lower between the years 2010 and 2018. Perhaps this is an indicator that higher education costs will still increase, but at a much lower rate to accommodate for incoming college students.

In the plot, I made a green, dashed vertical line to denote the year (2012) when I started my undergraduate studies at Ohio State. As one would expect, those fees are slightly higher than those from the 2010 term. If I were to use the graph as my barometer for the 2012 fees, I would expect the fees to have been between $4200 and $4300 for that term. Based on my current student loan balance, this would not be too surprising.

In this project, there were a few minor challenges. I have never created a vertical line with an annotation on a plot before, which required me to do some Google research to make sure I was constructing the correct line for the year 2012. In addition, there were some initial formatting issues with labeling the axes and title, but those matters were resolved quickly.

In this analysis, Motor Trend magazine gather information on the horsepower and mileage for 32 cars in the 1973-1974 model year. In order to determine a relationship between the variables of horsepower and mileage, I created a scatterplot using the two variables.

There appears to be a negative correlation between the variables. As the amount of horsepower increases, the mileage of the car decreases. Likewise, as the amount of mileage increases, the horsepower of the car decreases. The best fit function for the data would not be a linear function, but most likely a quadratic or logarithmic function.